Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Трапеция
основание
ГЛ
основание
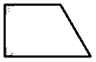
прямоугольная
трапеция
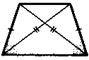
равнобокая
трапеция
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны1. Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами.
Трапеция называется равнобокой, если у нее равны боковые стороны.
Трапеция называется прямоугольной, если у нее есть прямой угол.
Свойства равнобокой трапеции
1. Углы при основании равнобокой трапеции равны.
2. Диагонали равнобокой трапеции равны.
Признаки равнобокой трапеции
1. Если углы при основании трапеции равны, то она равнобокая.
2. Если диагонали трапеции равны, то она равнобокая.
1. Назовите в русском языке существительное, однокоренное слову трапеция.
2. Середина основания трапеции равноудалена от концов другого основания. Обязательно ли данная трапеция равнобокая?
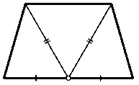
3. Докажите свойства равнобокой трапеции.
4. Докажите первый признак равнобокой трапеции.
5. Докажите второй признак равнобокой трапеции.
6. Существует ли трапеция, длины оснований которой равны 2 и 6, а длины боковых сторон 1 и 5?
7. Постройте трапецию по длинам всех ее сторон.
8. Постройте трапецию по длинам ее оснований и диагоналей.
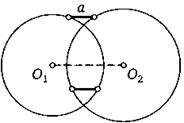
9. Даны две пересекающиеся окружности разных радиусов. Постройте отрезок данной длины а с концами на этих окружностях, параллельный линии их центров. Сколько решений может иметь задача?
10. Углы при одном основании трапеции равны 50° и 80°. Докажите, что одна из ее боковых сторон равна разности оснований.
11. Один из углов трапеции в два раза больше противоположного. Найдите боковую сторону при данном угле, если основания трапеции равны а и Ъ.
а
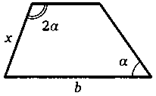
12. Существуют ли две такие трапеции, что боковые стороны каждой из них равны основаниям другой?
13. Каждая диагональ трапеции равна сумме ее оснований. Найдите угол между ее диагоналями.
14. Постройте трапецию по длинам ее оснований и диагоналей.
15. Разрежьте трапецию на две части, из которых можно сложить треугольник.
16. Разрежьте трапецию на две части, из которых можно сложить параллелограмм.
17. Биссектриса одного угла трапеции делит ее боковую сторону пополам. Найдите другую боковую сторону трапеции, если основания равны а и Ъ.
а
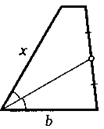
18. Боковая сторона трапеции равна а. Параллельно ей через середину другой боковой стороны провели прямую. Какой отрезок этой прямой заключен внутри трапеции?
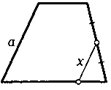
19. Середина боковой стороны трапеции равноудалена от двух противоположных от нее вершин. Докажите, что трапеция прямоугольная.
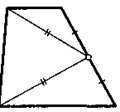
20. Биссектриса угла между основанием и первой диагональю трапеции делит вторую ее диагональ пополам. Найдите первую диагональ трапеции, если ее основания равны а и Ь.
21. Середины боковых сторон трапеции соединили с противоположными вершинами так, как показано на рисунке. Могут ли полученные два отрезка лежать на параллельных прямых?
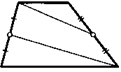
22. Произвольную точку М внутри равностороннего треугольника АВС соединили с вершинами. Докажите, что на каждой стороне треугольника можно выбрать по одной точке так, чтобы расстояния между ними были равны AM, ВЫ и СМ.
*23. Любую точку М внутри равнобокой трапеции ABCD соединили со всеми вершинами. Докажите, что из отрезков AM, ВМ, СМ и DM можно составить четырехугольник, вписанный в данную трапецию.
К задаче 2

К задаче 4