Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Прямоугольник, ромб, квадрат
Прямоугольником называется параллелограмм, все углы которого прямые.
Свойства прямоугольника
1. Диагонали прямоугольника равны.
2. Прямоугольник можно вписать в окружность.
Признаки прямоугольника
1. Если у параллелограмма равны диагонали, то он — прямоугольник.
2. Если параллелограмм можно вписать в окружность, то он — прямоугольник.
Ромбом называется параллелограмм, у которого равны все стороны.
Свойства ромба
1. Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.
2. В ромб можно вписать окружность2.
Признаки ромба
1. Если диагонали параллелограмма перпендикулярны, то он — ромб.
2. Если в параллелограмм можно вписать окружность, то он — ромб.
Квадратом называется параллелограмм, у которого равны все стороны и все углы. Квадрат является правильным четырехугольником3. Из определения очевидно, что квадрат одновременно является и прямоугольником, и ромбом.
1. Докажите первый признак прямоугольника.
2. Докажите, что при пересечении двух «полос» одинаковой ширины всегда образуется ромб. Под шириной полосы понимается расстояние между параллельными прямыми.
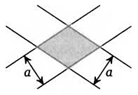
3. Середины сторон параллелограмма образуют ромб. Докажите, что данный параллелограмм — прямоугольник.
4. Середины сторон параллелограмма образуют прямоугольник. Докажите, что данный параллелограмм — ромб.
5. Докажите второй признак прямоугольника.
6. Вершина параллелограмма равноудалена от середин двух его сторон. Докажите, что этот параллелограмм — ромб.
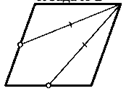
7. На каждой стороне квадрата взяли по точке так, что отмеченные на рисунке отрезки равны. Докажите, что четыре отмеченные точки сами образуют квадрат.
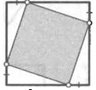
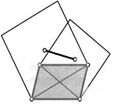
8. Вершины квадрата соединили отрезками с серединами сторон так, как показано на рисунке. Докажите, что закрашенная на рисунке фигура — квадрат.
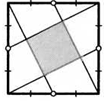
9. В квадрате провели два перпендикулярных отрезка так, как показано на рисунке. Докажите, что они равны.
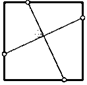
10. На сторонах параллелограмма вне его построили квадраты. Докажите, что их центры тоже образуют квадрат.
11. На стороне ромба построили равносторонний треугольник. Докажите, что радиус отмеченной на рисунке окружности равен стороне ромба.
12. Две соседние вершины квадрата «скользят» по сторонам прямого угла. Докажите, что его центр все время находится на биссектрисе этого угла.
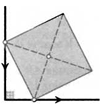
13. В данный параллелограмм впишите ромб так, чтобы на каждой стороне параллелограмма находилось по одной вершине ромба, причем одна из них была в заданной точке. Всегда ли это возможно?
14. На каждой диагонали параллелограмма построили по квадрату. Докажите, что расстояние между центрами квадратов равно одной из сторон параллелограмма.
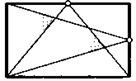
15. Отмеченные на рисунке точки — середины сторон прямоугольника. Докажите, что отмеченные на нем углы равны.
В С
16. На сторонах AD и CD квадрата ABCD взяли точки К и Е так, что угол АВК равен 15°, а угол EKD равен 30°. Найдите угол КВЕ.
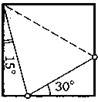
А К D
Е
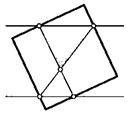
17. Две прямые, расстояние между которыми равно стороне квадрата, пересекают его стороны в четырех точках так, как это показано на рисунке. Найдите угол между двумя отмеченными отрезками, соединяющими эти точки.
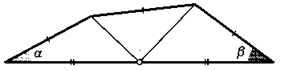
*18. Три стороны четырехугольника равны, причем одна из них (показанная на рисунке) видна под прямым углом из середины четвертой. Найдите сумму углов а + /3 при четвертой стороне.