Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Дополнительные построения, связанные с параллелограммом
1. Даны угол и точка М внутри него. Как провести через нее прямую так, чтобы отрезок этой прямой, заключенный внутри угла, делился точкой М пополам?
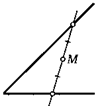
2. Сколько прямых, указанных в предыдущей задаче, можно провести через данную точку?
3. Внутри угла взяли точку. Как провести через нее прямую так, чтобы она проходила через вершину, если самой вершиной нельзя пользоваться?
4. Даны угол и некоторая прямая Z. Постройте прямую, параллельную Z, так, чтобы угол высекал на ней отрезок определенной длины.
5. Из середины стороны параллелограмма противоположная его сторона видна под прямым углом. Найдите отношение сторон параллелограмма.
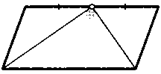
6. Разрежьте данный параллелограмм на две части, из которых можно составить треугольник.
7. Точка М —середина стороны CD параллелограмма ABCD. Точка К делит его сторону ВС на отрезки с длинами аиЬ так, что угол АМК — 90°. Найдите АК.
В а КЪ С В С
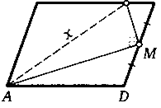
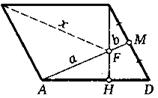
8. Вершину тупого угла А параллелограмма ABCD соединили с точкой М — серединой его стороны CD. Высота СН параллелограмма пересекает отрезок AM в точке F. Найдите BF, если AF = а, FM = b.
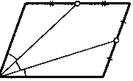
9. Вершину параллелограмма соединили с серединами двух его противоположных сторон. Могут ли равняться три отмеченных на рисунке угла?
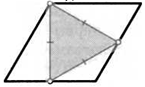
10. Вершина параллелограмма и середины двух его противоположных сторон образуют равносторонний треугольник. Найдите углы параллелограмма на рисунке.
11. Разбейте данный треугольник на две части так, чтобы из них можно было составить треугольник, не равный данному.
12. Медиана треугольника образует с его сторонами, выходящими из той же вершины, углы 40° и 70°. Докажите, что эта медиана равна половине одной из них.
13. Постройте треугольник по сумме двух его сторон, углу между ними и медиане, проведенной к третьей стороне.
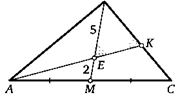
14. На медиане ВЫ треугольника АВС взяли точку Е. Прямая АЕ пересекает сторону ВС в точке К и образует равные углы с прямыми ВЫ и ВС. Найдите ВС, если BE = 5, ЕМ = 2.
В
15. У четырехугольника два противоположных угла равны, а соединяющая их диагональ делит другую пополам. Обязательно ли данный четырехугольник является параллелограммом?
А
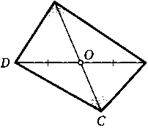
16. Диагональ четырехугольника разбивает его на два треугольника с равными периметрами. Другая диагональ пересекает ее в середине. Докажите, что данный четырехугольник —параллелограмм.
17. Диагонали разбивают четырехугольник на четыре треугольника равного периметра. Докажите, что данный четырехугольник — параллелограмм.
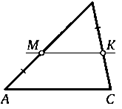
*18. Параллельно стороне АС треугольника АВС проведите прямую, которая пересекла бы его стороны АВ и ВС в таких точках М и К, что АМ = ВК.
В