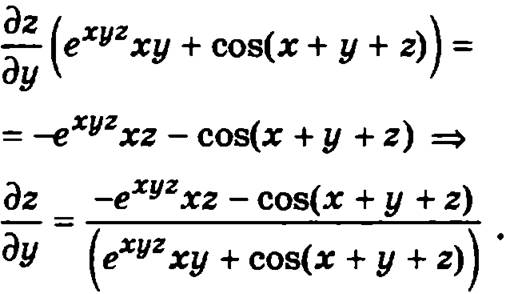Высшая математика мини-справочник для ВУЗов
Дифференцирование неявных функций - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть имеется неявно заданная функция F(x, y, z) = 0. Тогда частные производные в этом случае вычисляются по формулам:
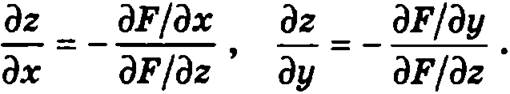
Пример. Найдем частные производные функции ехуz + sin(x + у + z) = 0.
Продифференцируем это равенство по х, учитывая, что переменная z зависит от х:
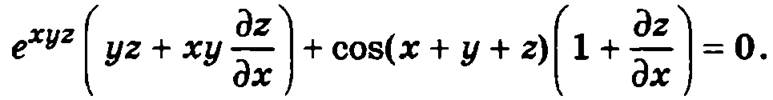
Из полученного соотношения выразим dz/dx:
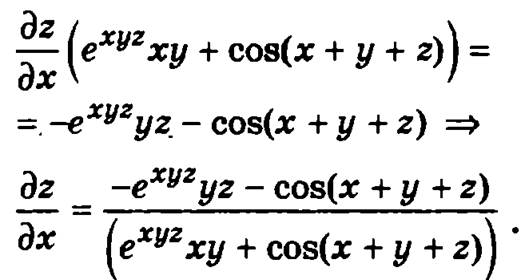
Аналогично, для того чтобы найти частную производную по у, продифференцируем соотношение exyz + sin(x + у + z) = 0 по у, учитывая, что z зависит от у
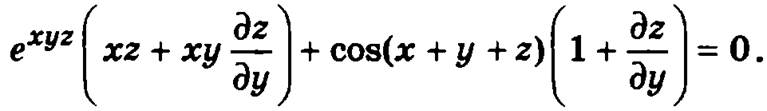
Тогда