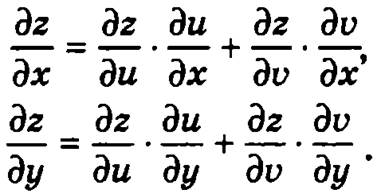Частные производные - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Упорядоченную совокупность вещественных чисел (x1, x2, ..., хn) будем называть точкой n-мерного пространства. Когдаx x1, x2, ..., хn принимают всевозможные значения, получают множества, которое называют Евклидовым n-мерным пространством.

Расстояние ρ(М1, М2) между двумя точками такого пространства М1(x1, x2, ..., хn) и М2(y1, y2, ..., yn) определяется формулой

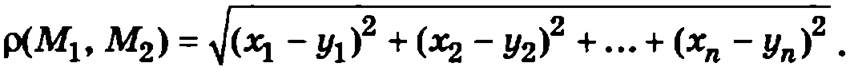
Обозначим через X некоторое множество, принадлежащее п-мерному Евклидому пространству, а через У — некоторое множество действительных чисел.

Определение. Говорят, что на множестве X задана функция нескольких переменных, если задан закон или правило, по которому каждой точке М из множества X ставится в соответствие некоторое число у из множества У:

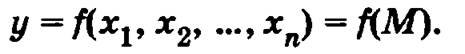
При этом множество X называется областью определения функции, а область У — областью изменения функции.

Определение. Число А называется пределом функции нескольких переменных у = f(M) при стремлении M(x1, x2, ..., хn) к точке M0(x10, x20, ..., хn0) (М → М0), если для любого ε > 0 существует такое число δ > 0, что неравенство |f(M) - А| < ε выполняется, как только ρ(М, М0) < δ

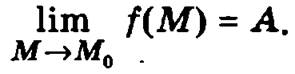
Определение. Функция у = f(М) называется непрерывной в точке М0, если она определена в этой точке и если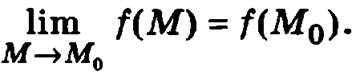

5.1. Частные производные

Далее будем для простоты рассматривать функцию двух переменных z = f(x, y) = f(М), учиты вая, что все излагаемое ниже справедливо и для функции любого количества переменных.

Пусть функция z = f(x, у) = f(М) определена на некотором множестве Q. Возьмем некоторую точку M0(x0, y0) ∈ Q и зафиксируем переменную у0, а переменной х0 дадим приращение ∆х такое, что точка М1(х0 + ∆х, у0) ∈ Q.

Разность ∆xf(x0, у0) = f(x0 + ∆х, y0) - f(х0, y0) называется частным приращением функции z = f(x, у) по переменной х в точке М0(x0, y0).

Определение. Если существует предел отношения частного приращения функции z = f(x, у) по переменной х в точке М0(х0, у0) к приращению переменной ∆х, то этот предел называют частной производной 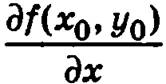функции z = f(x, у) по переменной х в точке М0(х0, у0):

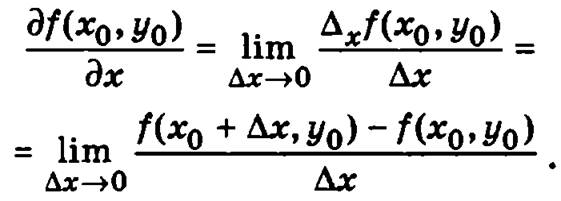
Аналогичным образом можно определить частную производную функции z = f(x, у) по переменной у в точке М0(x0, у0):

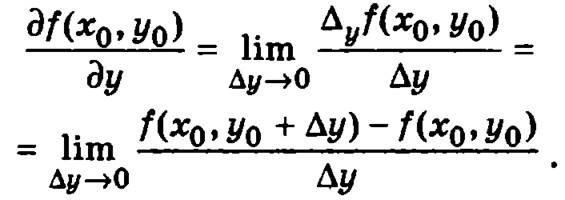
В соответствии с приведенными определениями отыскание частных производных функции по одной из переменных сводится к дифференцированию данной функции по этой переменной, при котором остальные переменные считаются постоянными.

Пример.

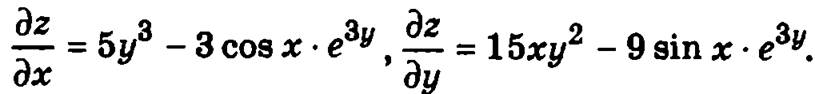
Если в точке М0(х0, у0) дать приращение обоим переменным таким образом, чтобы точка М2 (x0 + ∆х, y0 + ∆y) принадлежала области Q, то разность

называется полным приращением функции z = f(x, у) в точке М0(х0, у0).

Линейная относительно приращений независимых переменных ∆х и ∆у часть полного приращения функции z = f(x, у) в точке М0(х0, у0) называется полным дифференциалом df(x0, у0) функции z = f(x, y) в этой точке

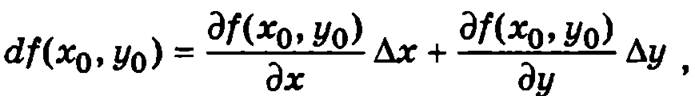
или учитывая, что ∆х = dx и ∆y = dy

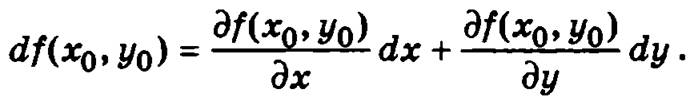
Частные производные от сложных функций

Пусть функция z = f(u, v) определена в области D, и каждая из переменных u и v представляет собой функции u = u(х, у и v = v(x, у) переменных х и у, определенные в области Q. В этом случае говорят, что на множестве Q задана сложная функция z = f(u(x, у), v(х, у)). Частные производные этой функции по переменным х и у вычисляются по формулам: