Вариант № 10 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. В некотором городе живёт 300 000 жителей, среди них 20% детей и подростков. Среди взрослых жителей 40% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?

В2. На диаграмме 66 показана месячная норма осадков для города Красноярска. По горизонтали указываются месяцы, по вертикали — количество осадков в мм. Определите месяц с наименьшей нормой осадков. В ответе запишите номер этого месяца.

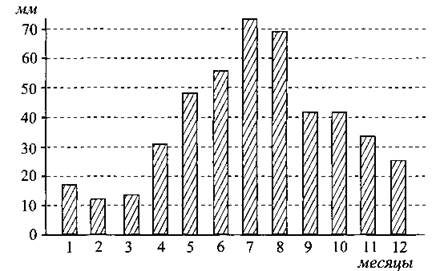
Рис. 66.

В3. Найдите площадь четырёхугольника, вершины которого имеют координаты (2; 6), (2; 9), (8; 5), (8; 2) (см. рис. 67).

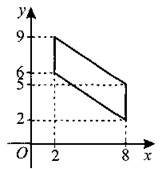
Рис. 67.

В4. Для транспортировки 49 тонн груза на 1800 км можно использовать услуги одного из трёх перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей для каждого перевозчика указаны в таблице. Сколько рублей будет стоить самая дешёвая перевозка (один рейс)?

Перевозчик	Стоимость перевозки одним автомобилем (руб. на 100 км)	Грузоподъёмность автомобилей (в тоннах)
А	3800	4,5
Б	6400	7
В	7200	9

В5. Найдите корень уравнения (х — 7)³ = 64.

В6. Найдите угол С ВО, если сторона ВС касается окружности, а меньшая дуга окружности АС, заключённая внутри этого угла, равна 67° (см. рис. 68). Ответ дайте в градусах.

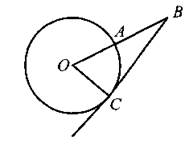
Рис. 68.

В7. Найдите значение выражения

В8. На рисунке 69 изображён график производной функции f(x), определённой на интервале (—8; 6). В какой точке отрезка [—2; 3] функция f(x) принимает наименьшее значение?

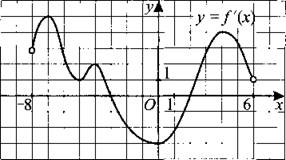
Рис. 69.

В9. Диагональ куба равна √48 (см. рис. 70). Найдите его объём.

Рис. 70.

В10. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в среду в автобусе окажется меньше 30 пассажиров, равна 0,92. Вероятность того, что окажется меньше 22 пассажиров, равна 0,61. Найдите вероятность того, что число пассажиров будет от 22 до 29.

В11. Боковые рёбра треугольной пирамиды взаимно перпендикулярны (см. рис. 71), каждое из них равно 6. Найдите объём пирамиды.

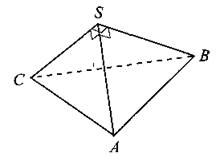
Рис. 71.

В12. В розетку подключены электроприборы, общее сопротивление которых составляет 120 Ом. Параллельно с ними в розетку планируется подключить электрообогреватель. Определите наименьшее возможное сопротивление обогревателя (в омах), если для нормального функционирования электросети общее сопротивление в ней должно быть не менее 30 Ом, а общее сопротивление проводников при параллельном подключении вычисляется по формуле где R₁ и R₂ — сопротивления этих проводников.

В13. Смешали некоторое количество 31%-го раствора с таким же количеством 23%-го раствора. Сколько процентов составляет концентрация получившегося раствора?

В14. Найдите точку минимума функции у = 5 + 6х + х².

Часть 2

С1. а) Решите уравнение

б) Найдите корни этого уравнения, принадлежащие промежутку (-7π/2; -2π).

С2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка Е — середина ребра СС₁. Найдите расстояние между прямыми АЕ и ВС₁, если АВ = 3, AD = 2, СС₁ = 4.

С3. Решите систему неравенств

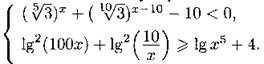
С4. На боковой стороне равнобедренного треугольника как на диаметре построена окружность, делящая вторую боковую сторону в отношении 2 : 3. Найдите основание треугольника, если его боковая сторона равна 15 см.

С5. Найдите все значения параметра а, при которых система уравнений

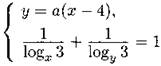
не имеет решений.

С6. Для натурального числа n S(n) — сумма всех его натуральных делителей, Q(n) — сумма всех обратных чисел к делителям числа n. Найдите n в каждом из следующих случаев: