Вариант № 9 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Больному прописано лекарство, которое нужно пить по 0,5 г 5 раз в день в течение 9 дней. В одной упаковке содержится 10 таблеток лекарства по 0,5 г. Какое наименьшее количество упаковок потребуется на весь курс лечения?

В2. На рисунке 61 показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 13 мая. Ответ дайте в градусах Цельсия.

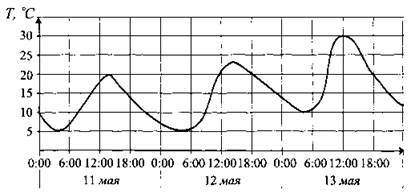
Рис. 61.

В3. Найдите площадь трапеции, вершины которой имеют координаты (1; 2), (1; 5), (10; 3), (10; 8) (см. рис. 62).

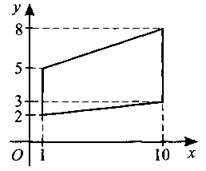
Рис. 62.

В4.В магазине компьютерной техники объявлена акция: если покупатель приобретает товар на сумму свыше 3 000 рублей, он получает сертификат на 500 рублей, который можно обменять в том же магазине на любой товар ценой не выше 500 рублей. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель Н. хочет приобрести наушники ценой 2600 рублей, клавиатуру ценой 450 рублей и компьютерную мышь ценой 300 рублей. В каком из возможных случаев Н. заплатит за покупку меньше всего?

1) Н. купит все три товара сразу.

2) Н. купит сначала наушники и клавиатуру, а компьютерную мышь получит за сертификат.

3) Н. купит сначала наушники и компьютерную мышь, клавиатуру получит за сертификат.

В ответе запишите, сколько рублей заплатит Н. за покупку в этом случае. В5. Найдите корень уравнения (х + 3)³ = —27.

В6. Найдите радиус R окружности, описанной около треугольника LMK, если стороны квадратных клеток равны 1 (см. рис. 63). В ответе укажите 2 ∙ R√5.

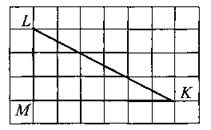
Рис. 63.

В7. Найдите sin а, если cos а = √15/4 и a ∈ (3π/2; 2π).

В8. На рисунке 64 изображён график производной функции f(x), определённой на интервале (—8; 6). Найдите точку максимума функции f(x) на отрезке [—5; 3].

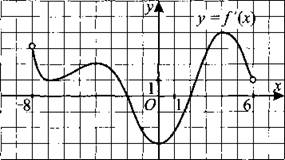
Рис. 64.

В9. Высота конуса равна 12, а диаметр основания — 10. Найдите образующую конуса.

В10. Вероятность того, что на тесте по физике Петя верно решит больше 8 задач, равна 0,78. Вероятность того, что Петя верно решит больше 7 задач, равна 0,85. Найдите вероятность того, что Петя верно решит ровно 8 задач.

В11. Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 30 (см. рис. 65). Найдите объём треугольной пирамиды D₁ACD.

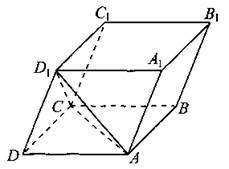
Рис. 65.

В12. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч², вычисляется по формуле Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав два километра, развить скорость не менее 120 км/ч. Ответ выразите в км/ч².

В13. Смешали 3 литра 12%-го водного раствора и 5 литров 20%-го водного раствора. Сколько процентов составляет концентрация получившегося раствора?

В14. Найдите точку максимума функции

Часть 2

С1. а) Решите уравнение

б) Найдите корни этого уравнения, принадлежащие промежутку (2π; 7π/2).

С2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка F — середина ребра DD₁, точка К лежит на ребре AD так, что АК : KD — 1:3. Найдите расстояние между прямыми BF и А₁К, если АВ = 3, AD = 4, АА₁ = 2.

С3. Решите систему неравенств

С4. Окружность, диаметр которой равен 2√3, проходит через соседние вершины А и В прямоугольника ABCD. Длина отрезка касательной, проведённой из точки С к окружности, равна 3, АВ = √3. Найдите сторону AD.

С5. Найдите все значения параметра а, при которых система уравнений

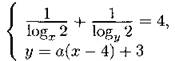
имеет ровно два различных решения.

С6. Последовательность {х_n} задана рекуррентной формулой. В каждом из следующих случаев определите наименьшее возможное значение │x_k│ по всем k, для которых определено x_k.

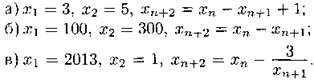Если некоторое х_j = 0, то х_m не определено для m > j.