Вариант № 11 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. В школе 1200 учеников, из них 16 февраля 5% отсутствовало на занятиях. Среди присутствовавших на занятиях учеников 40% обедало в школьной столовой. Сколько учеников обедали в школьной столовой в этот день?

В2. На рисунке 72 жирными точками показана цена акций компании «Сургутнефтегаз» на момент закрытия биржевых торгов во все рабочие дни января 2011 года. По горизонтали указываются числа месяца, по вертикали — цена акции в рублях. Для наглядности точки на рисунке соединены линией. Определите по рисунку, какого числа цена акции «Сургутнефтегаза» на момент закрытия торгов была наименьшей за данный период.

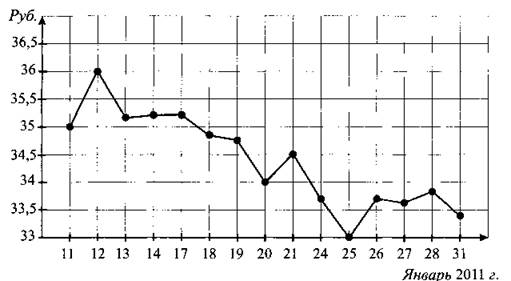
Рис. 72.

В3. Высота трапеции равна 15, а площадь — 225. Найдите среднюю линию трапеции.

В4. Для изготовления книжных полок библиотеке требуется заказать 64 одинаковых стекла в одной из трёх фирм. Площадь каждого стекла — 0,125 м². В таблице приведены цены на стекло, а также на его резку и шлифовку края. Сколько рублей будет стоить самый дешёвый заказ?

Фирма	Цена стекла (руб.за 1 м2)	Резка и шлифовка (руб. за одно стекло)
А	320	85
Б	360	75
В	440	50

В5. Найдите корень уравнения

В6. В треугольнике АВС угол С равен 90°, АВ = 10, АС = 8. Найдите тангенс угла А.

В7. Найдите значение выражения при n = 36.

В8. На рисунке 73 изображён график функции у = f(x), определённой на интервале (—8; 8). Определите количество целых точек, в которых производная функции положительна.

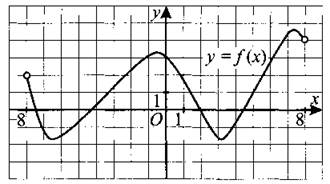
Рис. 73.

В9. В правильной треугольной пирамиде SABC R — середина ребра ВС, S — вершина (см. рис. 74). Известно, что АВ = 6, a SR = 9. Найдите площадь боковой поверхности.

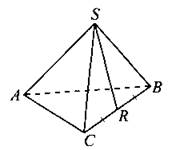
Рис. 74.

В10. Рядом находятся два банкомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого банкомата. Найдите вероятность того, что хотя бы один из этих банкоматов исправен.

B11. Объём одного шара в 64 раза больше объёма второго (см. рис. 75). Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Рис. 75.

В12. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой где T₁ — температура нагревателя (в градусах Кельвина), Т₂ — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя Т₁ КПД этого двигателя будет не меньше 20%, если температура холодильника Т₂ = 310 К? Ответ выразите в градусах Кельвина.

В13. Оля и Дима читают одну и ту же книгу. Оля читает за час 50 страниц, а Дима только 30. Дети начали читать книгу одновременно и не прерывались, при этом Оля закончила читать на 36 минут раньше. Сколько страниц текста содержит книга?

В14. Найдите точку максимума функции у = 6х² — х³.

Часть 2

С1. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку (-2π; -π/2).

С2. В правильной треугольной призме АВСА₁В₁С₁ сторона основания равна 4, высота — 10. Точки К и М — середины рёбер АС и А₁В₁ соответственно. Найдите косинус угла между прямыми АС₁ и КМ.

С3. Решите систему неравенств

С4. Окружность с центром, О проходит через вершины А и В треугольника АВС и пересекает луч С А в точке М и луч СВ в точке N. ∠AOM = ∠BON = 60°, расстояние от точки N до прямой АВ равно 10. Найдите площадь ∆АВС, если длины MN и АВ отличаются в 4 раза.

С5. Найдите все значения параметра а, при которых система имеет хотя бы одно решение.

С6. Разбившись на бригады, 30 школьников пошли собирать яблоки. После окончания сбора школьники каждой бригады делят между собой поровну собранные этой бригадой яблоки, а остаток от такого деления (если он есть) отправляют в общий котёл, где будет вариться компот (котёл один на все 30 человек). Всего в саду на деревьях росло 336 яблок, и все они были собраны. Какое наибольшее число яблок может оказаться в котле, если:

а) в каждой бригаде 6 человек;

б) в бригадах может быть любое количество человек (причём в разных бригадах — разное)?