Поурочные разработки по Алгебре 8 класс
Урок 1 - ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Цели: ввести понятие иррациональных уравнений, равносильных уравнений; объяснить правило решения иррациональных уравнений и показать оформление решения; формировать умение решать иррациональные уравнений.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Выставить оценки за самостоятельную работу. Задания, по которым было допущено наибольшее количество ошибок, рассмотреть на доске.
В а р и а н т 1
Задание 3.
Найдите коэффициент k для уравнения x2 – kx – 3 = 0, если один из его корней равен 3.
Р е ш е н и е:
По теореме Виета:
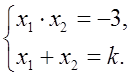
Один из корней равен 3, значит 3x1 = –3; x1 = –1.
Найдем коэффициент k = 3 + (–1) = 2.
О т в е т: k = 2.
В а р и а н т 2
Задание 3.
Найдите коэффициент k для уравнения x2 + 6x + k = 0, если один из его корней равен –2.
Р е ш е н и е:
Применим теорему Виета:
X1 + x2 = –6;
X2 = –6 – x1 = –6 + 2 = –4.
Также с помощью теоремы Виета найдем неизвестный коэффициент:
![]()
О т в е т: k = 8.
Тем учащимся, которые получили отрицательные оценки, домой задаются аналогичные самостоятельной работе задания.
1) Решить уравнения:
а) x2 – 4x – 32 = 0; б) 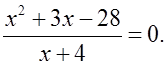
2) Сократить дробь: 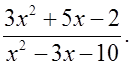
3) Найдите коэффициент k для уравнения x2 + kx + 15 = 0, если один из его корней равен –3.
III. Объяснение новой темы.
Данная тема объясняется согласно параграфу. Рассмотреть на доске решение иррационального уравнения:
![]()
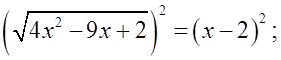
4x2 – 9x + 2 = x2 – 4x + 4;
3x2 – 5x – 2 = 0;
D = b2 – 4ac = 25 + 24 = 49 = 72;
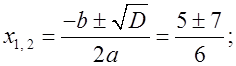
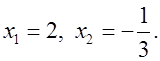
Проверка:
1) При х = 2 получим 2) При 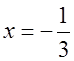 получим
получим
![]()
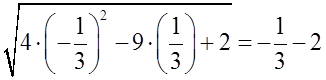 (неверно),
(неверно),
![]() подкоренное значение не может быть отрицательным
подкоренное значение не может быть отрицательным
![]()
0 = 0 (верно). ![]() – посторонний корень.
– посторонний корень.
О т в е т: 2
IV. Закрепление нового материала.
1) Какие из данных чисел 2, –3, 1, 0, 5 являются корнями уравнения:
а) ![]()
б) ![]()
в) ![]()
2) Какие из данных уравнений не имеют корней:
а) ![]() б)
б) ![]()
в) ![]() г)
г) 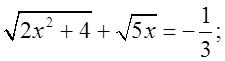
д) ![]() е)
е) ![]()
3) Разобрать № 30.2; 30.4; 30.8; 30.10; 30.12; 30.16.
V. Подведение итогов.
Домашнее задание: решить задачи № 30.1; 30.7; 30.11.