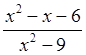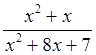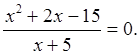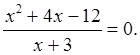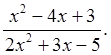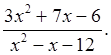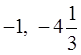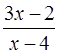Поурочные разработки по Алгебре 8 класс
Урок 3 - ТЕОРЕМА ВИЕТА
Цели: повторить правила разложения многочлена на множители; развивать умение решать квадратные уравнения различными способами, раскладывать многочлены на множители, сокращать дроби.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
К доске вызываются четыре ученика для самостоятельного решения заданий с карточек:
Карточка 1 Разложить на множители многочлен: x2 – 4x + 3. |
Карточка 2 Разложить на множители многочлен: 5x2 – 3x – 2. |
Карточка 3 Сократить дробь: |
Карточка 4 Сократить дробь: |
III. Актуализация знаний.
Пока на доске решаются задания с карточек, остальные учащиеся самостоятельно разбирают задание № 29.18.
Затем комментируются решения заданий из тетрадей, проверяются индивидуальные задания и домашняя работа.
IV. Решение задач.
1) Разбираются задания № 29.21; 29.22; 29.24; 29.34; 29.40.
Задания для сильных учеников.
2) Пусть x1 и x2 корни заданного квадратного трехчлена. Найдите значения выражения f(x1, x2).
а) x2 – 7x – 1, 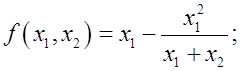
б) x2 – 4x – 1, ![]()
3) Пусть x1 и x2 корни заданного уравнения x2 + 13x – 17 = 0.
Составьте квадратное уравнение, корнями которого являлись бы числа 2 – x1 и 2 – x2.
V. Самостоятельная работа.
Вариант 1 |
Вариант 2 |
1) Решите данные уравнения: |
|
а) x2 + 4x – 12 = 0; б) 3x2 + 8x – 3 = 0; в) |
а) x2 – 4x – 21 = 0; б) 5x2 – 8x + 3 = 0; в) |
2) Сократите дробь
|
2) Сократите дробь
|
3) Найдите коэффициент k для уравнения x2 – kx – 3 = 0, если один из его корней равен 3. |
3) Найдите коэффициент k для уравнения x2 + 6x + k = 0, если один из его корней равен –2. |
О т в е т ы:
Задание |
1 (а) |
1 (б) |
1 (в) |
2 |
3 |
I |
2 и – 6 |
|
3 |
|
|
II |
7 и – 3 |
1,8 и 1,4 |
2 и – 6 |
|
|
VI. Подведение итогов.
Домашнее задание: решить задачи № 29.23; 29.25; 29.28; 29.33.