Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Дробно-линейная функция и ее график (факультативное занятие) - Числовые функции
Цель: рассмотреть свойства дробно-линейной функции и ее график.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Определение корня n-й степени из числа а.
2. Найдите значение выражения ![]()
3. Постройте график функции ![]()
Вариант 2
1. Определение арифметического корня n-й степени из числа а.
2. Найдите значение выражения ![]()
3. Постройте график функции ![]()
III. Изучение нового материала
Ранее были рассмотрены свойства и график функции ![]() при разных k. Графиком функции является гипербола. Особенностью этого графика является наличие вертикальной и горизонтальной асимптот. Асимптотой графика функции y(x) называют прямую, к которой неограниченно близко приближается (при определенных условиях) график функции >>(х). По внешнему виду асимптоты разделяются на вертикальные, горизонтальные и наклонные.
при разных k. Графиком функции является гипербола. Особенностью этого графика является наличие вертикальной и горизонтальной асимптот. Асимптотой графика функции y(x) называют прямую, к которой неограниченно близко приближается (при определенных условиях) график функции >>(х). По внешнему виду асимптоты разделяются на вертикальные, горизонтальные и наклонные.
Значения функции ![]() при малых значениях х(х → 0) неограниченно возрастают (у → ∞) или убывают (у → -∞). Поэтому при малых х график функции неограниченно близко приближается коси ординат (прямой x = 0). Такая прямая является вертикальной асимптотой графика функции
при малых значениях х(х → 0) неограниченно возрастают (у → ∞) или убывают (у → -∞). Поэтому при малых х график функции неограниченно близко приближается коси ординат (прямой x = 0). Такая прямая является вертикальной асимптотой графика функции ![]() .
.
При больших значениях |х| (|х| → ∞) значения функции стремятся к нулю (у → 0). Поэтому при больших значениях |x| график функции ![]() неограниченно близко приближается к осиабсцисс (прямой у = 0). Такая прямая является горизонтальной асимптотой графика функции
неограниченно близко приближается к осиабсцисс (прямой у = 0). Такая прямая является горизонтальной асимптотой графика функции ![]() .
.
Теперь обобщим функцию ![]() и рассмотрим функцию
и рассмотрим функцию ![]() где х - переменная; а, b, с, d - некоторые числа, причем с ≠ 0 и ad - bc ≠ 0. Такую функцию называют дробно-линейной, т. е. формула, задающая функцию, представляет собой дробь, числитель и знаменатель которой линейные функции. Очевидно, что при a = d = 0 и
где х - переменная; а, b, с, d - некоторые числа, причем с ≠ 0 и ad - bc ≠ 0. Такую функцию называют дробно-линейной, т. е. формула, задающая функцию, представляет собой дробь, числитель и знаменатель которой линейные функции. Очевидно, что при a = d = 0 и ![]() дробно-линейная функция
дробно-линейная функция ![]() является обратно пропорциональной зависимостью
является обратно пропорциональной зависимостью ![]() .
.
Пример 1
Следующие функции являются дробно-линейными:
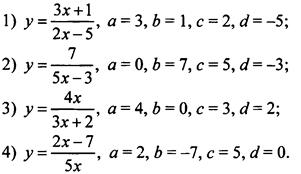
Заметим, что приведенные ограничения важны. При с - 0 дробно-линейная функция ![]() является линейной:
является линейной: ![]() при ad - bc = 0: константой
при ad - bc = 0: константой ![]()
Можно показать, что графиком дробно-линейной функции ![]() является гипербола, которую можно получить с помощью параллельных переносов вдоль координатных осей графика
является гипербола, которую можно получить с помощью параллельных переносов вдоль координатных осей графика ![]() . Для этого в дробно-линейной функции надо выделить целую часть, т. е. представить ее в виде
. Для этого в дробно-линейной функции надо выделить целую часть, т. е. представить ее в виде ![]() (где n, k, m - некоторые числа).
(где n, k, m - некоторые числа).
Пример 2
Построим график функции ![]()
В дроби ![]() выделим целую часть и представим функцию в виде
выделим целую часть и представим функцию в виде ![]() Здесь n = 2, k = -1, m = 1. Таким образом, надо построить график функции
Здесь n = 2, k = -1, m = 1. Таким образом, надо построить график функции ![]()
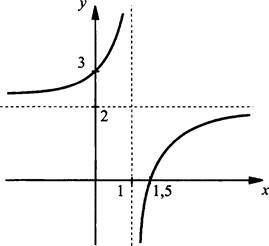
Он получается смещением гиперболы ![]() на одну единицу вправо и на две единицы вверх. График данной функции имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = 2.
на одну единицу вправо и на две единицы вверх. График данной функции имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = 2.
Пример 3
Рассмотрим еще один способ построения графика дробно-линейной функции ![]()
Для этого найдем точки пересечения графика функции с осями координат. Положим х = 0 и определим точку пересечения с осью ординат: ![]() Теперь положим у = 0, получим уравнение:
Теперь положим у = 0, получим уравнение: ![]() или 0 = 2х - 3 - и найдем точку пересечения с осью абсцисс х = 1,5. Построим точки A(0; 3) и B(1,5; 0).
или 0 = 2х - 3 - и найдем точку пересечения с осью абсцисс х = 1,5. Построим точки A(0; 3) и B(1,5; 0).
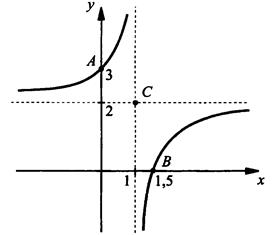
Определим асимптоты графика функции. Вертикальную асимптоту находим из условия, что функция не определена, т. е. х - 1 = 0, откуда х = 1. Поведение функции при больших значениях |x| (|х| → ∞) определяет горизонтальную асимптоту. При таких значениях х в числителе дроби ![]() можно пренебречь числом (-3), в знаменателе - числом (-1). Тогда получаем горизонтальную асимптоту
можно пренебречь числом (-3), в знаменателе - числом (-1). Тогда получаем горизонтальную асимптоту ![]() Построим асимптоты графика х = 1 и у = 2.
Построим асимптоты графика х = 1 и у = 2.
При построении графика функции учтем:
1) ветви графика (гиперболы) симметричны относительно точки С пересечения асимптот;
2) график функции не пересекает асимптот.
После этих замечаний легко построить график данной функции.
Пример 4
Построим график функции ![]()
Раскроем знак модуля и получим: 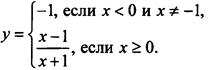 При отрицательных значениях х и х ≠ -1 построим горизонтальную прямую у = -1. При х ≥ 0 строим график дробно-линейной функции
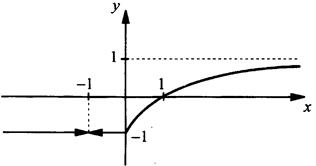
При отрицательных значениях х и х ≠ -1 построим горизонтальную прямую у = -1. При х ≥ 0 строим график дробно-линейной функции ![]() Этот график пересекает ось ординат в точке у = -1 и ось абсцисс в точке x = 1. График имеет горизонтальную асимптоту у = 1. График также имеет вертикальную асимптоту х = -1, но она в рассматриваемый промежуток х ≥ 0 не входит. Таким образом, график данной функции состоит из прямой с удаленной точкой (-1; -1) и части гиперболы.
Этот график пересекает ось ординат в точке у = -1 и ось абсцисс в точке x = 1. График имеет горизонтальную асимптоту у = 1. График также имеет вертикальную асимптоту х = -1, но она в рассматриваемый промежуток х ≥ 0 не входит. Таким образом, график данной функции состоит из прямой с удаленной точкой (-1; -1) и части гиперболы.
Пример 5
Построим график функции ![]()
Раскрыв знаки модуля, получим: 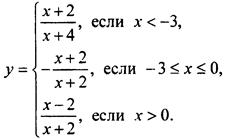
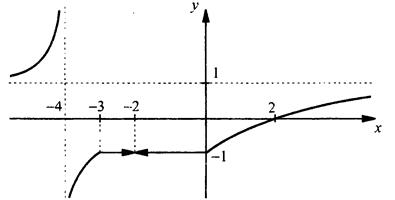
Построим полученные зависимости. На промежутке х ∈ (-∞; - 3) гипербола ![]() имеет вертикальную асимптоту х = -4, ось 0х не пересекает. На промежутке х ∈ [-3; 0] функция
имеет вертикальную асимптоту х = -4, ось 0х не пересекает. На промежутке х ∈ [-3; 0] функция ![]() определена всюду, за исключением точки х = -2. При этом у = -1. На промежутке х ∈ (0; +∞) гипербола
определена всюду, за исключением точки х = -2. При этом у = -1. На промежутке х ∈ (0; +∞) гипербола ![]() имеет горизонтальную асимптоту y = 1 и пересекает ось 0х в точке х = 2. Учитывая вышесказанное, нетрудно получить график исходной функции.
имеет горизонтальную асимптоту y = 1 и пересекает ось 0х в точке х = 2. Учитывая вышесказанное, нетрудно получить график исходной функции.
Пример 6
При каком значении параметра а прямая у = ax + 1 касается гиперболы ![]() Найдем координаты точки касания.
Найдем координаты точки касания.
Очевидно, что координаты точки касания удовлетворяют системе уравнений 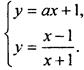 При этом система должна иметь единственное решение. Приравняем правые части и получим уравнение:
При этом система должна иметь единственное решение. Приравняем правые части и получим уравнение: ![]() или ax2 + х + ах + 1 = х - 1, или ах2 + ах + 2 = 0 (очевидно, что а ≠ 0). Чтобы это квадратное уравнение имело один корень, его дискриминант D = а2 - 8а = 0, откуда а = 8. Найдем координаты точки касания. Подставим значение а = 8 в уравнение ах2 + ах + 2 = 0 и получим: 8х2 + 8х + 2 = 0 или 2(2х + 1)2 = 0, откуда х = -1/2. Найдем соответствующее значение
или ax2 + х + ах + 1 = х - 1, или ах2 + ах + 2 = 0 (очевидно, что а ≠ 0). Чтобы это квадратное уравнение имело один корень, его дискриминант D = а2 - 8а = 0, откуда а = 8. Найдем координаты точки касания. Подставим значение а = 8 в уравнение ах2 + ах + 2 = 0 и получим: 8х2 + 8х + 2 = 0 или 2(2х + 1)2 = 0, откуда х = -1/2. Найдем соответствующее значение ![]() Итак, координаты точки касания графиков [-1/2; -3].
Итак, координаты точки касания графиков [-1/2; -3].
IV. Контрольные вопросы
1. Приведите графики функции у = k/x для k > 0 и для k < 0.
2. Понятие асимптоты графика функции.
3. Определение дробно-линейной функции.
4. Способы построения графика дробно-линейной функции.
5. Нахождение асимптот графика дробно-линейной функции.
V. Задание на уроках
§ 10, № 19 (а, б); 23 (в, г); 24 (а, б).
VI. Задание на дом
§ 10, № 19 (в, г); 23 (а, б); 24 (в, г); 27.
VII. Творческие задания
1. Постройте график функции:
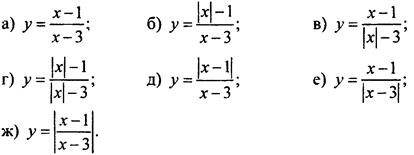
2. Постройте график уравнения:
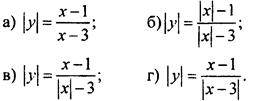
3. Постройте график функции y(х). При каких значениях параметра а уравнение a = у(х) не имеет решений?
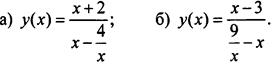
Ответы: a) a = 0, a = 1/2, a = 1; б) a = -1, a = -1/2, a = 0.
VIII. Подведение итогов уроков