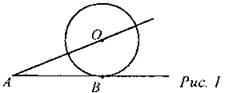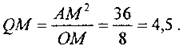ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМЕ ОКРУЖНОСТЬ - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ

Цель деятельности учителя

Создать условия для систематизации знаний по теме “Окружность”, повторения основных свойств, признаков окружности, для подготовки к сдаче ГИА

Термины и понятия

Окружность и круг, касательная к окружности и ее свойства; окружность, описанная около треугольника; окружность, вписанная в треугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений

Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; владеют логическими действиями определения понятий, обобщения, установления аналогий.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Задания для математического диктанта, групповой работы, домашней работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Задания для математического диктанта

Проверить навыки решения простых задач из вариантов ГИА

(И) Математический диктант с самопроверкой.

1. К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 12 см, АО = 13 см.

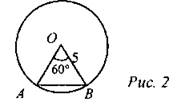
Ответ: 5.

2. Центральный угол АОВ равен 60°.

Найдите длину хорды АВ, на которую он опирается, если радиус окружности равен 5.

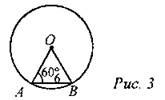
Ответ: 5.

3. Центральный угол АОВ опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°.

Найдите радиус окружности.

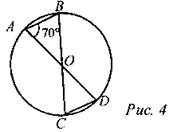
Ответ: 6.

4. В окружности с центром в точке О проведены диаметры AD и ВС, угол ОАВ равен 70°.

Найдите величину угла OCD.

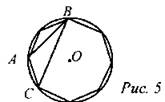
Ответ: 70.

5. В окружность вписан равносторонний восьмиугольник.

Найдите величину угла АВС.

Ответ: 22,5

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Проверить умение решать задачи повышенной сложности

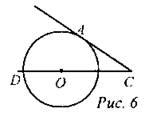
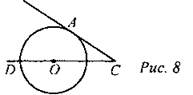
(Г) Учащимся предлагаются задачи из второй части ГИА.

На решение отводится 20 минут, затем каждая группа презентует решение одной задачи. После обсуждения решения записывают в тетрадь.

1. Найдите угол АСО, если его сторона СА касается окружности, О - центр окружности, а дуга ADокружности, заключенная внутри этого угла, равна 100°.

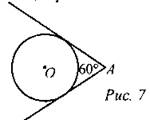
2. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

3. Найдите угол АСО, если его сторона СА касается окружности, О - центр окружности, а дуга ADокружности, заключенная внутри этого угла, равна 140°.

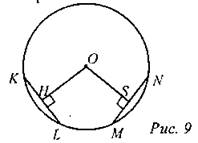
4. В окружности с центром О проведены две равные хорды KL и MN. На эти хорды опущены перпендикуляры ОН и OS. Докажите, что ОН и OS равны.

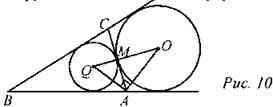
5. Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и основания АС. Найдите радиус окружности, вписанной в треугольник АВС.

Решение:

1. Проведем радиус ОА. Треугольник AОС - прямоугольный,

∠A = 90°. ∠COA = 180° - ∠AOD = 180° - 100° = 80°;

∠ACO = 90° - 80°= 10°.

Ответ: 10.

2. Опустим радиусы на каждую касательную. Соединим точки А и О. Получившиеся треугольники - прямоугольные, так как радиус, проведенный в точку касания, перпендикулярен касательной. По гипотенузе и катету эти треугольники равны, таким образом, мы получили, что угол, лежащий напротив катета, равен 30°. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, тогда радиус равен 4.

Ответ:4.

3. Проведем радиус ОА. Треугольник АОС - прямоугольный, ∠А = 90°. ∠СОА = 180° - ∠AOD = 180° - 140° = 40°; ∠АСО = 90 - 40° = 50°.

Ответ: 50°.

4. Проведем OK, ON, ON, ОМ - радиусы. Треугольники KOLи MON равны по трем сторонам, тогда высоты ОН и OSтакже равны как элементы равных треугольников, что и требовалось доказать.

5. Пусть О - центр данной окружности, a Q - центр окружности, вписанной в треугольник АВС (рис. 10). Точка касания окружностей Мделит АС пополам. AQ и AO - биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AМ²= MQ ∙ МО.

Следовательно,

Ответ: 4,5

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что повторили на уроке?

- Оцените свою работу и работу группы.

- Закончите фразы:

• Я понял...

• Я вспомнил...

• Я научился...

• Я воодушевился...

(И) Домашнее задание: решить задачи:

1. Хорда АВ окружности радиуса 4 см видна из центра под углом 90°. Найдите: 1) хорду АВ и расстояние от центра окружности до этой хорды;

2) углы треугольника АВС, где С - точка, расположенная на большой дуге АВ окружности так, что ∪АС : ∪СВ = 5 : 4; 3) хорду ВС.

2. Две взаимно перпендикулярные хорды АВ и СВ окружности пересекаются в точке К, причем АК = 6 см, ВК = 32 см, KD = 24 см.

Найдите: 1) хорды BD и CD; 2) расстояние от точки А до прямой BD; 3) радиус данной окружности.

3. Треугольник АВС с углом В, равным 135°, вписан в окружность с центром О и радиусом R = 10√2 см.

Найдите: 1) сторону АВ; 2) сторону АВ и S_АВС, если известно, что угол АСВ равен 30°