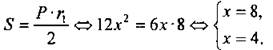ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМЕ ОКРУЖНОСТЬ - Урок 2 - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ

Цель деятельности учителя

Создать условия для систематизации знаний по теме “Окружность”, повторения основных свойств, признаков окружности, для подготовки к сдаче ГИА

Термины и понятия

Окружность и круг, касательная к окружности и ее свойства; окружность, описанная около треугольника; окружность, вписанная в треугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений

Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; владеют логическими действиями определения понятий, обобщения, установления аналогий.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Задания для математического диктанта, групповой работы, домашней работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить уровень сформированности теоретических знаний

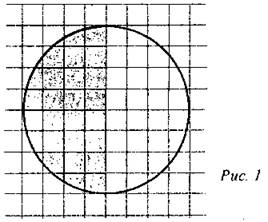
(Ф/И)

1. Проверка правильности выполнения домашнего задания.

Три ученика выносят на доску решение домашних задач. Остальные учащиеся сверяют со своим решением и задают интересующие их вопросы по выполненной работе.

2. Математический диктант.

- Какие из следующих утверждений верны?

1) Центром окружности, описанной около правильного треугольника, является точка пересечения высот.

2) В любой четырехугольник можно вписать не более одной окружности.

3) Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него окружности равен 5.

4) Сумма смежных углов равна 90°.

5) Через любые две различные точки проходит не более одной прямой.

6) Через любые две различные точки проходит не менее одной прямой.

Ответы: 1, 3, 5.

3. Решение задач (устно).

1) Найдите (в см²) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис 1).

В ответе запишите S/π.

2) Один острый угол прямоугольного треугольника в 9 раз больше другого. Найдите больший острый угол. Ответ дайте в градусах.

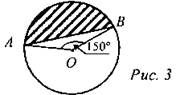
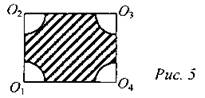
3) Найти площадь заштрихованной фигуры, если R = 6.

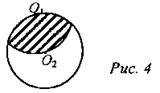
4) R₁ = R₂ = 5. Найти площадь заштрихованной фигуры.

5) Найти площадь заштрихованной фигуры.

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать

навыки решения

задач

(Ф/И) и (Г)

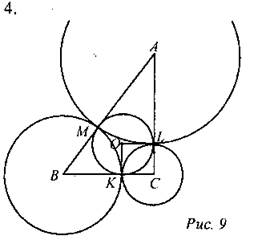
X. Угол ВАС равен углу ВСР, так как ∠ВАС = 90° - ∠АВС и ∠BCP = 90° - ∠ABC. Так как тангенс - это отношение противолежащего катета к прилежащему, имеем: Тогда BP = 4х, PC = 3х, а гипотенуза ВС = 5х по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на радиус вписанной окружности, но площадь прямоугольного треугольника равна половине произведения катетов, следовательно, имеем:

Таким образом, BP = 16, PC = 12, а ВС = 20.

Так как то АС = 15, а АВ = 25 по теореме Пифагора.

В треугольнике АВС площадь равна произведению половины его периметра на радиус вписанной в него окружности, но площадь прямоугольного треугольника равна половине произведения катетов, следовательно, имеем:

Ответ: r = 5.

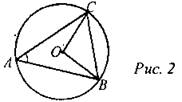
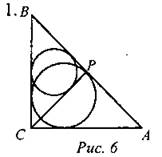
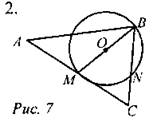
Медиана ВМ делит АС пополам. Центр окружности лежит на середине медианы ВМ, тогда ON - средняя линия в треугольнике ВМС, где О - центр окружности, а N - точка пересечения этой окружности стороны ВС. Средняя линия в треугольнике равна половине основания, поэтому ON = 1. Средняя линия ON является радиусом окружности. Так как медиана ВМ является диаметром, то ВМ = 2ON = 2. Проведем MN в треугольнике ВМС. Так как угол BNM опирается на диаметр ВМ, то ∠BNM = 90°, таким образом, треугольник BNM - прямоугольный. Так как MN - средняя линия, то она параллельна АВ, тогда треугольник АВС - прямоугольный. Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, таким образом, радиус описанной вокруг треугольника АВС окружности равен 2.

Ответ: r = 2.

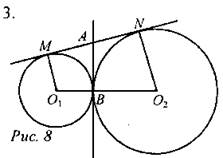
Обозначим центры первой и второй окружностей за O₁ и O₂, а точки касания с общей касательной, не проходящей через точку В, за М и N. Прямоугольные треугольники АО₁М и АО₁В равны по катету и гипотенузе. Аналогично, равны треугольники AО₂N и АО₂В. Значит, прямые О₁А и О₂А являются биссектрисами углов МО₁В и NО₂B соответственно. Прямые МО₁ и NО₂параллельны, поэтому сумма углов МО₁В и NO₂B равна 180°, а сумма углов АО₁В и АО₂В равна 90°, то есть треугольник О₁О₂А - прямоугольный. Поскольку АВ - высота, проведенная к гипотенузе, треугольники АО₁В и АО₂В подобны. Значит,

Ответ: 9.

Стороны треугольника, вершинами которого являются центры этих трех окружностей, равны 5, 12 и 13.

Поскольку 5² + 12² = 13², этот треугольник прямоугольный. Площадь этого треугольника равна 30. В то же время, она равна произведению радиуса вписанной окружности на полупериметр. Значит, искомый радиус равен

Ответ: 2

Этот этап урока можно провести в форме деловой

игры. Класс делится на четыре группы. Две группы выступают в роли экспертов, а другие две группы - в роли выпускников, сдающих ГИА. Затем группы меняются ролями.

Задачи для групп:

1. Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР, равен 8, тангенс угла ВАС равен 4/3. Найдите радиус окружности, вписаннойв треугольник АВС.

2. Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в ее середине. Длина стороны АС равна 4. Найдите радиус описанной окружности треугольника АВС.

3. Окружность радиуса 4 касается внешним образом второй окружности в точке В. Общая касательная к этим окружностям, проходящая через точку В, пересекается с некоторой другой их общей касательной в точке А. Найдите радиус второй окружности, если АВ = 6.

4. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трех окружностей

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И) Подвести итоги экспертной деятельности.

- Какие бы баллы вы поставили друг другу при решении данных задач?

- Что получилось? Что не получилось?

- Что было самым сложным?

(И) Домашнее задание: повторить тему “Многоугольники и четырехугольники”.

Решить задачи:

1. Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АС, равен 3 см, К - точка касания окружности с боковой стороной, КВ = 4.

Найдите: 1) сторону АС; 2) угол ВАС; 3) радиус окружности, описанной около треугольника АВС.

2. В равнобедренный треугольник АВС с основанием АС вписана окружность, касающаяся сторон АВ и ВС в точках М и Н.

1) Докажите, что ∆МВН ~ ∆АВС.

2) Найдите угол ВАС и радиус окружности, если АВ = 2 м, МН = 1 м