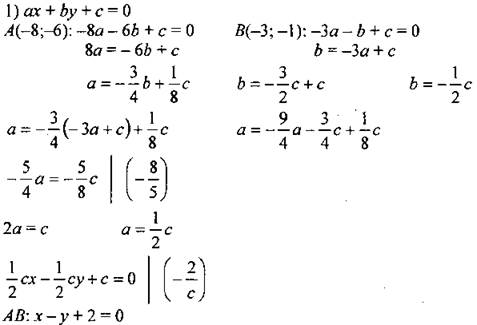Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
РЕШЕНИЕ ЗАДАЧ - МЕТОД КООРДИНАТ
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач |
||||
|
Термины и понятия |
Прямая, уравнение прямой, окружность, уравнение окружности, метод координат |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом, навыками устных, письменных, инструментальных вычислений; умеют применять метод координат |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: понимают и сохраняют учебную задачу; умеют контролировать процесс и результат учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группе. Личностные: проявляют познавательный интерес к изучению учебного предмета |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||||
|
Образовательные ресурсы |
• Задания для групповой работы; • задания для математического диктанта |
||||
|
I этап. Актуализация заданий учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Выявить трудности, возникшие при выполнении домашнего задания; определить уровень знаний по теме |
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Проверить решение № 979. 3. Провести математический диктант. Вариант I 1. Лежит ли точка А(2; -1) на окружности, заданной уравнением (x - 2)2 + (у - 3)2 = 25? 2. Напишите уравнение окружности, если ее центр - точка (4; 5), а радиус равен 3. 3. Напишите уравнение прямой, проходящей через точку М(3; -2) и параллельной оси ординат. 4. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С(-2; 3). 5. Напишите уравнение прямой, проходящей через две точки М(-2; -1) и N(3; 1). 6. Найдите длину вектора 7. Найдите координаты середины отрезка PQ, если Р(5; -3); Q(3; -7). 8. Найдите координаты вектора Вариант II 1. Лежит ли точка А(2; -1) на прямой, заданной уравнением 2х - 3у - 1 = 0? 2. Напишите уравнение окружности, если ее центр - точка (4; 5), а радиус равен 2. 3. Напишите уравнение прямой, проходящей через точку N(-2; 3) и параллельной оси абсцисс. 4. Напишите уравнение прямой, проходящей через начало координат и точку D (3; -2). 5. Напишите уравнение окружности с центром в точке Р(-2; -1), если она проходит через точку Q(1; 3). 6. Найдите расстояние между точками А(-1; 3) и В(2; -1). 7. Найдите координаты вектора 8. Найдите координаты вектора |
№ 979. Дано: M є АВ; А(-8; -6), В(-3; -1) и М(5; у). Найти: у. Решение:
2) Так как М є АВ, то ее координаты удовлетворяют уравнению 5 - у + 2 = 0; у = 7, отсюда: М(5; 7) Ответ: 7 |
|||
|
II этап. Решение задач |
|||||
|
Цель деятельности |
Задания для групповой деятельности |
||||
|
Совершенствовать навыки решения задач |
(Г) Класс разбивается на несколько групп. Каждая группа решает задачу в течение 10 минут. Далее следует презентация выполненной работы. 1-я труп па: Найдите площадь треугольника, ограниченного прямыми у - х = 0, у + х = 0, у - 2х + 4 = 0. 2-я группа: Докажите, что линия, заданная уравнением х2 + 8х + у2 - 6х - 24 = 0, является уравнением окружности. Найдите расстояние от центра окружности до прямой, параллельной оси ординат и проходящей через точку (5; -6). 3-я группа: Найдите площадь треугольника, образованного осями координат и прямой, проходящей через точки A(1; 10) и B(-1; -4). 4-я группа: 1) Напишите уравнение прямой, проходящей через точку В(-3; 10) и перпендикулярной оси Оу. 2) Принадлежат ли точки А(3; -5) и В(4; 2) прямой 7х - 5у - 18 = 0? 3) Выясните взаимное расположение прямой у = 30 и окружности (х - 5)2 + (у - 10)2 = 100 |
||||
|
III этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Оцените свою работу и работу группы. - Что оказалось для вас наиболее сложным? |
(И) Домашнее задание: 958, 944, 945, 998 |
||||