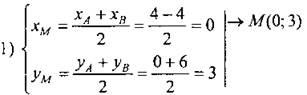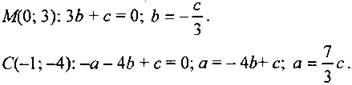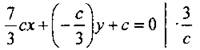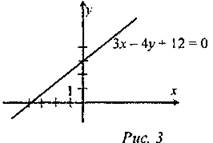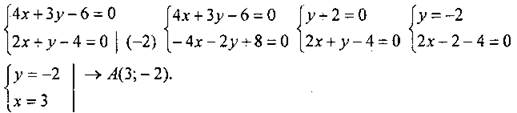УРАВНЕНИЕ ПРЯМОЙ - МЕТОД КООРДИНАТ

Цель деятельности учителя

Создать условия для выведения уравнения прямой

Термины и понятия

Прямая, уравнение прямой

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом, навыками устных, письменных, инструментальных вычислений; умеют применять метод координат

Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения, формулировать выводы.

Регулятивные: понимают и сохраняют учебную задачу; умеют контролировать процесс и результат учебной деятельности.

Коммуникативные: понимают и воспринимают на слух объяснение учителя.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Задачи для фронтальной работы

I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при выполнении домашнего задания

(Ф)

1. Ответить на вопросы учащихся.

2. Продемонстрировать решение № 1002 (б) (один ученик у доски).

3. Провести самостоятельную работу (контролирующая, 10-15 мин).

Вариант I

Решить задачи № 959 (г), 968, 960 (б).

Вариант II

Решить задачи № 959 (в), 967, 960 (в)

II этап. Изучение нового материала

Цель деятельности

Задания для самостоятельной работы

Вывести уравнение прямой

(И)

Учащиеся самостоятельно работают по учебнику.

Для более продвинутых учащихся обязателен вывод уравнения прямой, для менее подготовленных - только формула

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(И/Ф)

1. Решить на доске и в тетрадях № 973, 975, 976.

2. Решить устно задачи.

1) Окружность задана уравнением (х - 1)² + у² = 9. Назвать уравнение прямой, проходящей через ее центр и параллельной оси ординат.

2) Окружность задана уравнением (x + 1)² + (у - 2)² = 16.

Назвать уравнение прямой, проходящей через ее центр и параллельной оси абсцисс

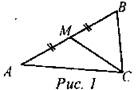
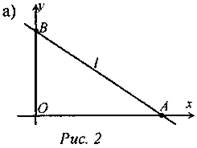
№ 973.

Дано: A(4; 6); В(-4; 0); С(-1; -4), СМ- медиана ∆АВС.

Написать уравнение прямой СМ.

Решение:

2) Так как М(0; 3) и С(-1; -4) лежат на прямой 1, заданной уравнением ах + by + с = 0, то их координаты должны удовлетворять этому уравнению.

Подставим значения b и а в исходное уравнение.

7x – y + 3 = 0 — искомое уравнение.

№ 975.

Дано: l: 3х - 4у + 12 = 0.

Найти: А(х; у); B(xi; yi).

Решение:

а) если l ∩ Ох = А, то А(х; 0), следовательно, 3х - 4 ∙ 0 + 12 = 0,

3x = -12,

х = -4, следовательно, А(-4; 0).

б) Если l ∩ Оу = В, то B(0; у), следовательно,

3 ∙ 0 - 4у + 12 = 0,

4у = 12,

у = 3, следовательно, B(0; 3).

№ 976.

Дано: l₁: 4х + 3у - 6 = 0; l₂: 2х + у - 4 = 0; l₁ ∩ l₂ = А.

Найти: А(х; у).

Решение:

1) Решение:

Центр О (1; 0) и параллельная оси OY прямая x = 1.

2) Решение:

Центр А (-1; 2); прямая у = 2 параллельна оси ОХ

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- С какой темой познакомились на уроке?

- Зачем уравнение прямой изучается в геометрии?

(И) Домашнее задание: повторить материал пунктов 93-95; изучить материал пункта 96; вопросы 1-21, с. 244-245; решить задачи № 972 (б), 979; записать в тетрадях и разобрать решение задачи № 984 (уч., с. 243)