СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ - ВЕКТОРЫ

Цель деятельности учителя

Создать условия для введения понятия средней линии трапеции и доказательства теоремы о средней линии трапеции

Термины и понятия

Трапеция, средняя линия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять векторы при доказательстве теоремы о средней линии трапеции

Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения, выводы.

Регулятивные: умеют осуществлять контроль по результату и способу действий на уровне произвольного внимания и вносить необходимые коррективы.

Коммуникативные: выстраивают аргументацию, участвуют в диалоге.

Личностные: проявляют критичность мышления

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Задания для индивидуальной работы

I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при выполнении домашнего задания

(Ф/И)

1. Обсудить вопросы учащихся по домашнему заданию.

2. Ответить на вопросы:

1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и противоположно направленные векторы.

2) Какой вектор называется произведением данного вектора на данное число?

3) Могут ли векторы быть неколлинеарными?

4) Сформулируйте основные свойства умножения вектора на число

II этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие средней линии трапеции и доказать соответствующую теорему

(Ф/И)

1. Определение трапеции. Виды трапеций.

2. Определение средней линии трапеции.

3. Доказательство теоремы о средней линии трапеции (проводитучитель).

При доказательстве теоремы целесообразно использовать результат задачи 2, решенной на предыдущем уроке

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навык решения задач

(Ф/И)

1. Решить на доске и в тетрадях задачу № 793.

2. Решить задачу № 795.

3. Решить задачу № 799 на доске и в тетрадях

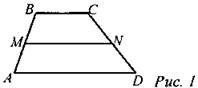
№ 793.

Дано: ABCD - трапеция, АВ = 13 см, СВ = 15 см, Р_ABCD = 48 см. М - середина АВ. N - середина CD. Найти: MN.

Решение:

1) P_ABCD = АВ + ВС + CD + AD, Р = 48 см, АВ = 13 см, СВ = 15 см, значит, ВС + AD + 13 + 15 = 48; ВС + AD = 48 - 28; ВС + AD = 20.

2) Средняя линия трапеции равна полусумме оснований, значит,

Ответ: 10 см.

№ 795.

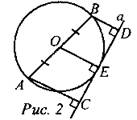
Дано: окружность с центром в точке О, АВ - диаметр, а - касательная к окружности (касается в точке Е), BD ⊥ а, АС ⊥ а, АС = 18 см, BD = 12 см.

Найти: АВ.

Решение:

1) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, поэтому ОЕ ⊥ a.

2) АС ⊥ a и В ⊥ a, значит, АС ll BD, то есть ABCD - трапеция.

3) ОЕ ⊥ а, АС ⊥ a, BD ⊥ а, значит, ОЕ ll АС ll BD и АО = ОВ (как радиусы), значит, по теореме Фалеса СЕ = ED, а это означает, что ОЕ - средняя линия трапеции ABCD.

4) Средняя линия трапеции ABCD равна полусумме оснований, поэтому

5) ОЕ = 15 см и ОЕ - радиус, значит, диаметр АВ = 2 ∙ ОЕ = 2 ∙ 15 = 30 (см).

Ответ: 30 см.

№ 799.

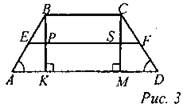
Дано: ABCD - равнобедренная трапеция, AB = CD, BK ⊥ AD, KD = 7.

Найти: среднюю линию.

Решение:

1) EF - средняя линия трапеции, EF ∩ ВК = Р, EF ∩ СМ = S (СМ ⊥ AD).

2) Пусть КМ = а, тогда ВС = а (так как КВСМ - прямоугольник). Пусть АК = b, тогда MD = b (тогда ∆АВК = ∆DCM по гипотенузе АВ = CD и острому углу ∠A = ∠D).

3) В ∆АВК ЕР - средняя линия, значит, ЕР = 1/2b.

4) В ∆DCM FS - средняя линия, значит, FS = 1/2b. EF ll ВС, значит, PS ⊥ ВК, PBCS - прямоугольник, PS = ВС = а.

5)

Ответ: 7

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали на уроке?

- Составьте синквейн к уроку

(И) Домашнее задание: решить задачи № 787, 794