Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ - НЕРАВЕНСТВА
Цели: изучить основные приёмы доказательства неравенств; сформировать умение доказывать сложные неравенства различными приёмами.
Ход урока
I. Актуализация знаний.
1. Сформулировать определение: число а больше числа b, если разность а - b - положительное число; число а меньше числа b, если разность а – b - отрицательное число.
2. Сформулировать основные свойства числовых неравенств:
Теорема 1. Если а > b, то b < а; если а < b, то b > а.
Теорема 2. Если а < b и b < с, то а < с.
Теорема 3. Если а < b и с - любое число, то а + с < b + с.
Теорема 4. Если а < b и с > 0, то ас < bс;
Если а < b и с < 0, то ас > bс.
Следствие. Если а > 0 и b > 0 и а < b, то ![]()
3. Сформулировать правила почленного сложения и умножения числовых неравенств.
Теорема 5. Если а < b и с < d, то а + с < b + d.
Теорема 6. Если а < b и с < d, где a, b, с, d - положительные числа, то ас < bd.
Следствие. Если а > 0, b > 0 и а < b, то аn < bn, где n є N.
II. Изучение нового материала.
1. Сначала показываем отличие заданий “решить неравенство” и “доказать неравенство”. В первом случае мы выполняем равносильные преобразования исходного неравенства, получаем более простое неравенство и находим те значения переменной, которые обращают неравенство в верное числовое неравенство (или доказываем, что таких значений нет).
В заданиях на доказательство неравенства в условии есть утверждение, что данное неравенство верно при любых значениях переменной либо при некоторых значениях (задано заранее множество значений переменной), и необходимо это утверждение доказать.
2. Доказательства проводятся с помощью различных приёмов, некоторые из которых знакомы учащимся.
1-й приём. Составляем разность левой и правой частей неравенства и показываем, что она сохраняет знак при любых указанных значениях переменных.
Рассматриваем данный приём на примере 1 со с. 193 учебника.
2-й приём. Показываем, что данное неравенство следует из других неравенств, справедливость которых известна.
К таким неравенствам (их ещё называют “основными” и “базовыми”) относятся:
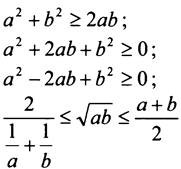 и др.
и др.
Рассматриваем данный приём на примере 2 со с. 193-194 учебника.
3-й приём. В отдельных случаях можно доказать неравенство, используя некоторые очевидные соотношения.
В качестве таких очевидных соотношений могут быть взяты, например, такие: ![]() при любом
при любом ![]() при
при ![]() при х ≥ -1 и т. п.
при х ≥ -1 и т. п.
Рассматриваем данный приём на примерах 3 и 4 со с. 194-195 учебника.
III. Формирование умений и навыков.
При доказательстве неравенств можно использовать любые предложенные приёмы, следует поощрять осознанный выбор того или иного приёма.
При рассмотрении задач на доказательство неравенств у учащихся может возникнуть представление об оторванности таких задач от потребностей практики. Чтобы этого не произошло, необходимо решать также прикладные задачи на неравенства.
№ 905 (а).
Составим разность:
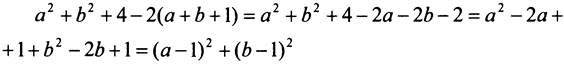
Имеем:
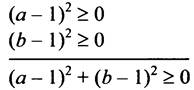 для любых а и и, значит,
для любых а и и, значит, ![]() Неравенство доказано.
Неравенство доказано.
№ 907 (а).
Составим разность
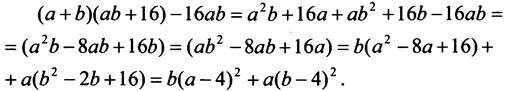
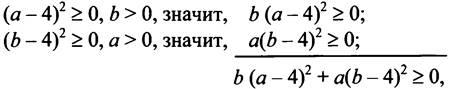
значит, ![]() при a > 0, b > 0. Неравенство доказано.
при a > 0, b > 0. Неравенство доказано.
№ 909.
Доказать, что ![]() для любых а > 0, b > 0.
для любых а > 0, b > 0.
![]()
Составим разность
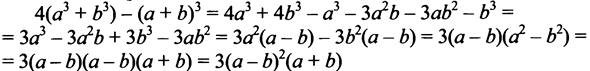
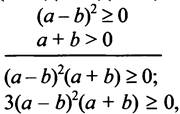 значит,
значит, ![]() неравенство доказано.
неравенство доказано.
№ 912.
Воспользуемся соотношениями.
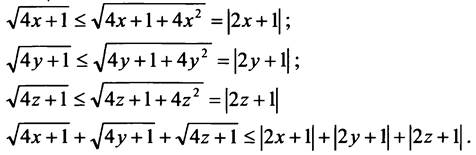
Имеем:
![]()
![]() значит,
значит, ![]()
Аналогично докажем, что ![]()
Имеем: ![]()
![]()
Значит, ![]() что и требовалось доказать.
что и требовалось доказать.
№ 914.
Анализ:
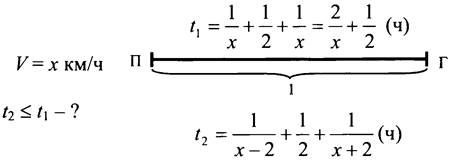
Пусть х км/ч - намеченная скорость велосипедиста, обозначим путь за 1, тогда, по расчетам, он должен был затратить ![]() на весь путь, а на самом деле затратил
на весь путь, а на самом деле затратил ![]()
Велосипедист успеет к сроку, если ![]() Докажем это.
Докажем это.
Составим разность:
![]()
![]() так как х > 2.
так как х > 2.
Имеем: ![]() значит, велосипедист не успел вернуться к назначенному сроку.
значит, велосипедист не успел вернуться к назначенному сроку.
Ответ: не успел.