Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ - Урок 2 - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: продолжить формирование умения решать дробные рациональные уравнения по алгоритму.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Найдите подбором корни уравнения:
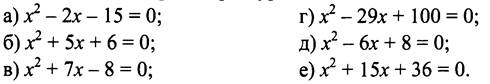
2. Решите уравнение:

III. Формирование умений и навыков.
Задания, предлагаемые учащимся на этом уроке, направлены на закрепление умения решать дробные уравнения по алгоритму.
1. Выполнение заданий: № 608 (б, г), 609 (а, б).
№ 608.
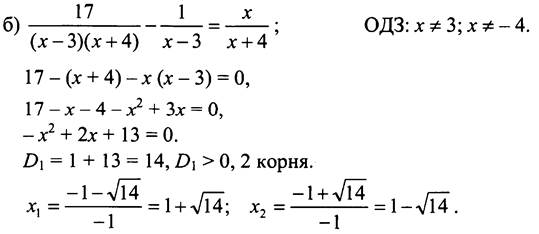
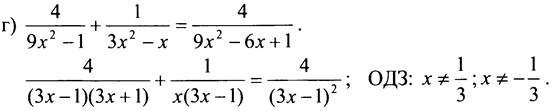
Общий знаменатель дробей ![]()
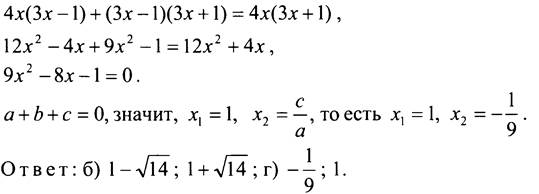
На этом примере наглядно демонстрируем учащимся необходимость разложения знаменателей на множители для последующего “составления” общего знаменателя.
№ 609.
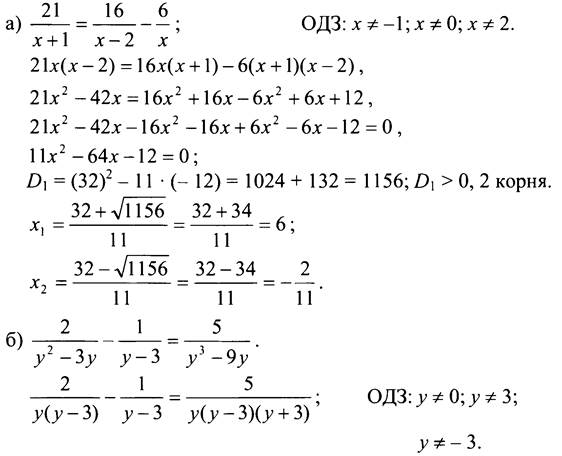
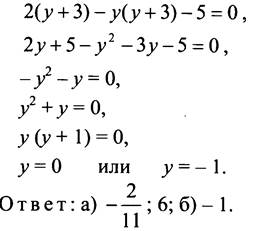
- Решите уравнения:
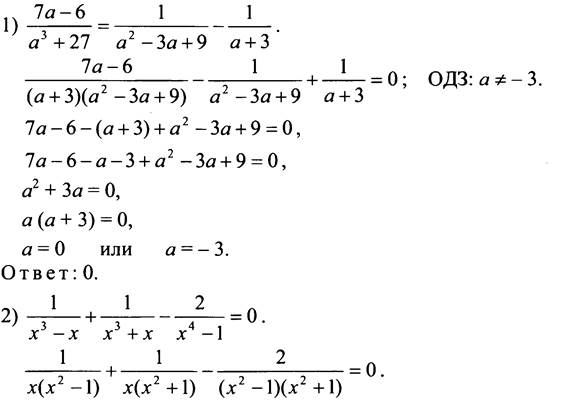
Общий знаменатель дробей ![]()
Домножим обе части уравнения на общий знаменатель:
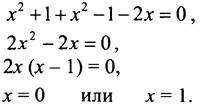
Если х = 0, то ![]()
Если х = 1, то ![]()
Ответ: нет решений.
№ 611 (б).
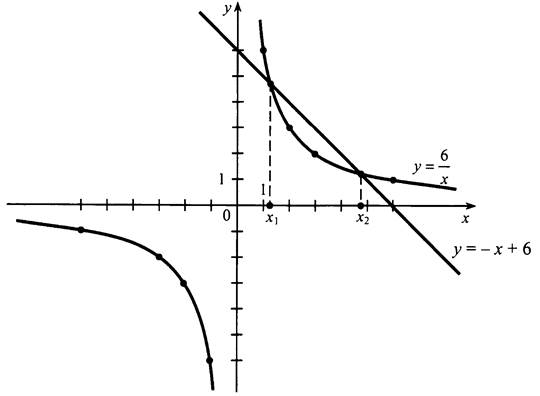
Графиком функции у = 6/x является гипербола, расположенная в I и III координатных четвертях. Запишем координаты контрольных точек:
|
x |
0,5 |
1 |
2 |
3 |
6 |
|
y |
12 |
6 |
3 |
2 |
1 |
Графиком функции у = -х + 6 является прямая, проходящая через точки (0; 6), (6; 0).
• Дополнительные задания повышенной трудности: № 610 (а), 612.
№ 610.
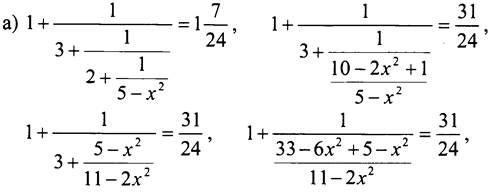
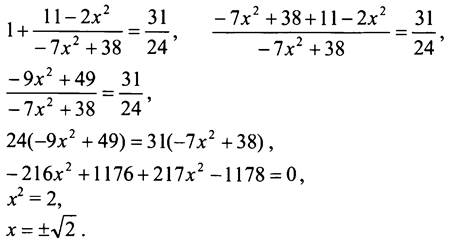
Оба корня удовлетворяют уравнению.
Ответ: ±√2.
IV. Итоги урока.
- Какие уравнения называются дробными рациональными?
- Каков алгоритм решения дробных уравнений?
- Как определить общий знаменатель дробей, входящих в уравнение?
- Каким способом можно исключить “посторонние” корни дробного рационального уравнения?
Домашнее задание: № 608 (а, в), 609 (в), 611 (а), 695 (д, з).