Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ПРИМЕНЕНИЕ ПОНЯТИЯ КВАДРАТНОГО КОРНЯ ПРИ РЕШЕНИИ РАЗЛИЧНЫХ ЗАДАЧ - КВАДРАТНЫЕ КОРНИ
Цели: продолжить формирование умения извлекать квадратные корни; формировать умение применять понятие квадратного корня при решении различных задач.
Ход урока
I. Организационный момент.
II. Проверочная работа.
Вариант 1
1. Найдите значение арифметического квадратного корня:
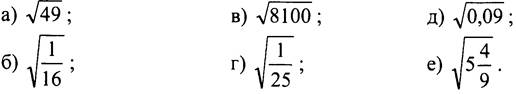
2. Найдите значение выражения:
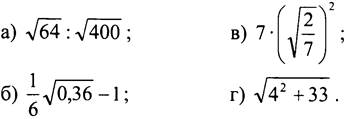
Вариант 2
1. Найдите значение арифметического квадратного корня:
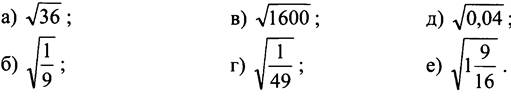
2. Найдите значение выражения:

III. Формирование умений и навыков.
Задания этого урока можно разделить на две группы:
1-я группа. Задания на нахождение значений квадратных корней: № 302, 307.
№ 307.
а) Чтобы значение выражения ![]() являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем три случая:
являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем три случая:
![]()
Эти же значения можно было найти подбором.
Ответ: 2; 7; 10.
2-я группа. Задания на решение простейших уравнений с квадратным корнем: № 310, 311, 312.
- Найдите значение переменной х, при котором верно равенство:
![]()
Решение
![]()
Нужно найти такое число, корень которого равен 3. Это число 9, то есть 2х - 1 = 9; 2х = 10; х = 5.
Нельзя допускать, чтобы учащиеся полагали, что при решении этого уравнения обе части возводятся в квадрат. Иначе, решая в дальнейшем, например, уравнение ![]() они перейдут к уравнению х + 1 = 4.
они перейдут к уравнению х + 1 = 4.

№ 315 (дополнительное задание).
Решение
Чтобы значение выражения ![]() являлось двузначным числом, необходимо выполнить два условия:
являлось двузначным числом, необходимо выполнить два условия:
1) корень из этого выражения должен извлекаться;
2) квадраты числа п и числа n2 + 39 должны отличаться на 39.
Пользуясь таблицей квадратов натуральных чисел, заметим, что, начиная с 20, квадраты чисел отличаются друг от друга более чем на 40. Значит, число n нужно искать среди чисел двух первых десятков.
Заметим, что только квадраты чисел 19 и 20 отличаются на 39; 192 = 361 и 202 = 400. Это означает, что n = 19. Получим:
![]()
Ответ: n = 19.
IV. Итоги урока.
- Что называется арифметическим квадратным корнем из числа а?
- Может ли подкоренное выражение быть отрицательным?
- Когда уравнение √х = а имеет решение? Сколько решений может иметь такое уравнение?
- Как решаются уравнения вида √х =а?
Домашнее задание: № 303, 313, 314, 466 (дополнительно).