РЕШЕНИЕ УРАВНЕНИЙ ВИДА х² = а - КВАДРАТНЫЕ КОРНИ

Цель: рассмотреть вопрос о количестве корней уравнения х² = а и формировать умение решать такие уравнения.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

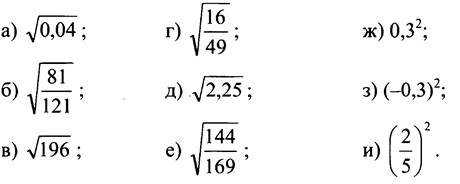
III. Объяснение нового материала.

Желательно, чтобы учащиеся самостоятельно решили вопрос о возможном количестве корней уравнения вида х² = а.

Задание: какие числа можно вписать в пустые карточки, чтобы равенство было верным?

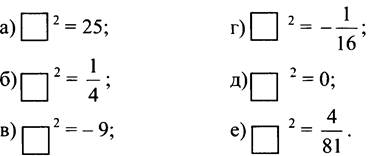
Рассмотрим уравнение х² = а. Сформулируйте утверждение о различных случаях, возникающих при поиске корней таких уравнений (запись выносится на доску):

Графическая интерпретация решения уравнения х² = а.

Вывод: если а > 0, то корнями уравнения х² = а будут числа √а и -√а.

IV. Формирование умений и навыков.

• № 319, 320,321 (а, в).

• Задание. Даны уравнения:

Выберите из них те, которые:

а) имеют два корня;

б) имеют два рациональных корня;

в) имеют два иррациональных корня;

г) имеют один корень;

д) не имеют корней.

• № 322.

• Задание. Составьте какое-нибудь уравнение, имеющее корни: а) 7 и -7; б) 0,2 и -0,2; в) √3 и -√3.

Соревнование: у кого из вас получится больше различных уравнений к каждому случаю?

Например, в первом случае можно составить такие уравнения:

х² = 49, 2х² = 98, х² + 1 = 50, 10 - х² = -39 и т. п.

• № 324 (а, в).

Образец оформления:

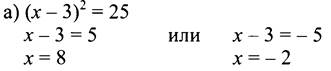
Ответ: -2; 8.

V. Итоги урока.

- Что называется арифметическим квадратным корнем из числа?

- Может ли в выражении 4а число а быть отрицательным? Почему?

- Сколько корней может иметь уравнение х² = а? От чего это зависит?

- Какие корни имеет уравнение х² = а, если а > 0; а = 0?

Домашнее задание: № 321 (б, г), 323, 324 (б, г).