Энергетическое описание движения колебательных систем. Решение задач - МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ - КОЛЕБАНИЯ И ВОЛНЫ

Задачи урока: продолжить отработку динамического описания колебательного движения; продолжить формирование умения применять закон сохранения полной механической энергии.

План урока

Этапы урока	Время, мин	Приёмы и методы
I. Актуализация знаний. Повторение II. Изучение и отработка нового материала III. Домашнее задание	7—10 30 1	Фронтальный опрос. Проверка домашнего задания Решение задач. Работа сучебником. Записи в тетрадях Запись на доске

I. В начале урока проводят проверку домашнего задания.

II. Изучение нового материала может быть организовано следующим образом. В механике, кроме использования законов Ньютона, при описании явлений широко используют закон сохранения импульса и закон сохранения энергии. Как использовать закон сохранения энергии для описания механических колебаний — основная учебная проблема урока.

1. Обсуждают вопросы: когда можно применить закон сохранения полной механической энергии? (Ответ. В случае если рассматриваемая система замкнутая.) Можно ли считать, что математический маятник и пружинный маятник — замкнутые системы? Вспоминают, что свободные колебания происходят под действием только внутренних сил. Выясняют, какова их природа.

2. Сначала рассматривают горизонтальный пружинный маятник (рис. 3.1 учебника). Записывают закон сохранения энергии. Для этого выбирают два “удобных” состояния системы. Первое состояние — амплитудное отклонение (А) груза от положения равновесия; второе — момент прохождения грузом положения равновесия.

Для первого состояния полная энергия равна:

Для второго состояния полная энергия будет равна:

Для произвольного состояния полная энергия равна:

В итоге закон сохранения может быть записан в виде

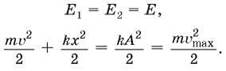
Вопросы для организации беседы: в каком состоянии системы потенциальная энергия груза максимальна? В каком состоянии кинетическая энергия максимальна? Почему при отпускании отклонённого маятника кинетическая энергия груза возрастает? Какую работу совершает сила упругости за период колебаний? Что происходит с энергией колебательной системы при уменьшении амплитуды колебаний? Как это доказать?

3. Записывают закон сохранения энергии для математического маятника. Состояния системы выбирают по аналогии с предыдущим случаем (рис. 46). В итоге получают

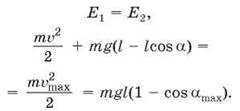
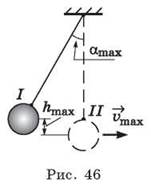
Учитель показывает на установке эти состояния колебательной системы.

4. К доске приглашают ученика для решения задачи.

Определите потерю энергии математическим маятником (рис. 47) за одно колебание, если до остановки маятник совершает 500 колебаний. Масса маятника равна 0,2 кг.

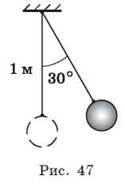
Заканчивается изучение нового материала решением фронтальной экспериментальной задачи.

Постройте график зависимости удлинения пружины от действующей силы, по графику определите работу силы, сравните её значение с потенциальной энергией растянутой пружины. Оборудование: пружина (или динамометр), штатив, линейка.

III. Домашнее задание: § 14; П., № 637. Индивидуально — задача.

Груз массой 0,1 кг подвесили на пружине жёсткостью 10 Н/м, отклонили от положения равновесия на 2 см и отпустили. Определите скорость груза в точке, находящейся на расстоянии 3 см от первоначального положения (рис. 48, а, б). Сопротивление воздуха не учитывайте.