Закон электромагнитной индукции - ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ - ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

Задачи урока: изучить закон электромагнитной индукции; ознакомить с использованием явления электромагнитной индукции на примере электродинамического микрофона; продолжить развитие мышления и формирование мировоззрения школьников.

План урока

Этапы урока	Время, мин	Приёмы и методы
I. Организационный момент II. Изучение нового материала: зависимость индукционного тока (и ЭДС индукции) от числа витков катушки и скорости изменения магнитного потока III. Закрепление изученного материала IV. Подведение итогов. Домашнее задание	1—2 20—25 15—20 2—3	Сообщение учителя Беседа. Эксперимент. Записи в тетрадях и на доске Решение экспериментальной задачи. Беседа. Наблюдение. Рассказ ученика Сообщение учителя

I. После организационного момента урока учитель ставит перед классом учебную проблему: установить количественную связь индукционного тока с изменением магнитного потока; иначе говоря, сформулировать закон электромагнитной индукции. Записывают тему урока. Затем переходят к решению проблемы.

Оборудование: два полосовых магнита, магнит подковообразный лабораторный, магнит от демонстрационного гальванометра, осциллограф, электродинамический микрофон, гальванометр демонстрационный, проводник длиной 1—1,2 м, два универсальных трансформатора, провода, выпрямитель, цветные мелки. На классной доске заранее должны быть подготовлены рисунки и схемы.

II. Изучение нового материала организуется поэтапно.

1. Решают экспериментальную задачу.

Предложите способ, который позволит обнаружить, какой из магнитов намагничен сильнее. Оборудование: два магнита (один — подковообразный лабораторный, другой — от демонстрационного гальванометра), катушка индуктивности, гальванометр, проводники.

Ученики отвечают, что надо по очереди опускать магниты в катушку одним и тем же полюсом, меняя магнитный поток. Стрелка будет отклоняться, и по отклонению стрелки гальванометра можно определить, какой магнит сильнее намагничен. Учитель рекомендует в опыте вдвигать магниты за одинаковое время Δt.

Ученик проводит опыт с магнитами, опуская их одним и тем же полюсом, а также разноимёнными полюсами. Делает вывод: сила индукционного тока прямо пропорциональна изменению магнитного потока, а изменение магнитного потока будет тем больше за одно и то же время Δt, чем сильнее намагничен магнит.

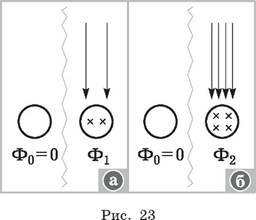
Учитель предлагает сделать зарисовку опыта на доске (рис. 23, а, б). Пусть вначале магнитный поток был Ф₀, затем при движении магнитов увеличили магнитный поток сначала до Ф₁, потом до Ф₂. Следовательно, изменение магнитного потока через одну и ту же площадку равно:

Итак, в опыте I₁ ~ ΔФ при Δt = const.

2. Вопрос: как вы думаете (выскажите гипотезу), можно ли увеличить силу индукционного тока, имея то же самое оборудование? (Ответ. Можно, если изменить время опускания магнитов в катушку.) Учитель просит показать это на опыте.

Ученик повторяет опыт, опуская магниты сначала медленно, а затем быстро.

Делают вывод: сила индукционного тока зависит от времени движения магнита при одинаковом изменении магнитного потока.

Вопрос: можно ли утверждать, что существует обратно пропорциональная зависимость силы индукционного тока от времени изменения магнитного потока? (Ответ. Да, можно.)

Как записать второй вывод на доске? (Ответ. ) Нельзя ли объединить эти два вывода? (Ответ. ) Не напоминает ли вам выражение выражение Как бы вы его назвали? (Ответ. Скорость.) Учитель говорит, что ответ верный, действительно, выражение называют скоростью изменения магнитного потока. Вопрос: как сформулировать вывод?

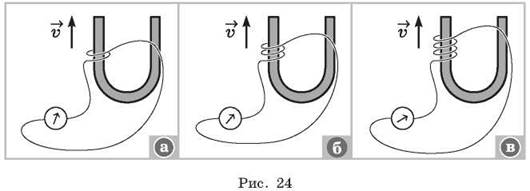
3. Так как класс работал с индукционной катушкой, на которой несколько сотен витков провода, то возникает вопрос: влияет ли число витков на силу индукционного тока? Повторяют один из опытов прошлого урока (рис. 24, а—в). Наблюдают возрастание ЭДС индукции при увеличении числа витков. Ученик поясняет, что существует прямая пропорциональная зависимость силы индукционного тока от числа витков. Учитель предлагает обозначить число витков буквой N и уточнить предыдущий вывод:

Делают вывод: сила индукционного тока в катушке пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром, и числу витков в катушке.

4. При изменении магнитного потока через поверхность контура в нём появляются сторонние силы, действие которых характеризуется ЭДС индукции:

Докажем это. По закону Ома при постоянном сопротивлении имеем Используя предыдущий вывод из двух выражений можно получить, что для контура из одного витка Так как коэффициент пропорциональности выбирают равным единице, то где ЭДС не зависит от свойств материала проводника.

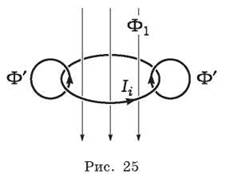
5. Вопрос: можно ли считать, что закон электромагнитной индукции получен в окончательном виде? (Ответ. Нет, так как не ясен знак .) Далее необходимо обратиться к рисунку известного опыта (см. рис. 18, а). (При необходимости эксперимент повторяют.) Через поверхность замкнутого контура возрастает магнитный поток. В контуре индуцируется ток I₁. Согласно правилу Ленца направление индукционного тока таково, что его магнитное поле Ф' противодействует нарастанию магнитного потока, вызвавшего этот ток (рис. 25). Поэтому < 0, и перед выражением надо поставить знак “минус”. Аналогично рассматривается случай, когда ΔФ < 0 (см. рис. 18, б).

Итак, величины и должны иметь противоположные знаки.

Согласно закону электромагнитной индукции ЭДС индукции в замкнутом контуре равна умноженной на количество витков скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком:

Данная формула закона полностью описывает явление электромагнитной индукции.

III. Для закрепления материала решают задачи методом эвристической беседы.

1. Как удвоить ЭДС во вторичной цепи, не изменяя её сопротивления? Собрана установка (рис. 26). Оборудование: трансформатор и катушки к нему, два ярма, выпрямитель ВС-24М, демонстрационный гальванометр, ключ, провода.

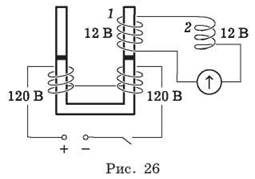
Решение. Катушка 2 может надеваться на сердечник; при этом активное сопротивление цепи не меняется. При замыкании ключа первичной цепи гальванометр показывает, например, два деления. Надеваем катушку 2 на сердечник 1 (не изменяя вторичной цепи). Показания прибора при отклонении стрелки равны четырём делениям шкалы. (Катушка надета так, что обозначение на ней 12 В оказывается перевёрнутым.)

2. При каком условии ЭДС во вторичной цепи равна нулю?

Решение. Перевернём катушку 2 на сердечнике 1, тогда

Учитель ставит вопрос: каково практическое значение закона электромагнитной индукции? (Ответ. В радиотехнике, электротехнике мы имеем дело с индукционными катушками.)

Затем класс знакомится с устройством и принципом действия электродинамического микрофона. Ученик по материалу учебника делает доклад, демонстрирует опыт.

IV. Домашнее задание: § 8, 9*; упр. на с. 42 (ЕГЭ); упр. на с. 45 (4). Индивидуально предлагается задача.

Определите ЭДС индукции в контуре ACDE (рис. 27), если проводник АС длиной 20 см движется со скоростью 10 см/с в магнитном поле с магнитной индукцией 0,1 Тл. Угол а равен 30°.

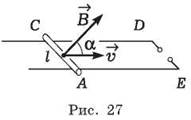
Решение. После краткой записи данных (анализ текста) выделяем физическое явление, которое рассматривается в задаче. Из рисунка видно, что магнитный поток изменяется за счёт изменения площади контура. Идея решения заключается в использовании закона электромагнитной индукции. Выражение для потока магнитной индукции следующее: Ф = BSsinα.

За время Δt площадь контура изменяется на ΔS = -lvΔt. Подставляя все данные в уравнение закона, получаем

При отсутствии замкнутого контура ЭДС в проводнике АС всё равно возникает. Её природа — действие силы Лоренца.