Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Кратчайшие пути
1. (Задача Герона из Александрии.) Точки А и В лежат по одну сторону от прямой. Постройте на этой прямой такую точку М, чтобы сумма отрезков AM + ВЫ была минимальна.
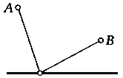
М
2. Точки А и В находятся по разные стороны от прямой. Найдите на этой прямой такую точку М, чтобы модуль разности \АМ—ВМ\ принимал наибольшее значение.
3. Докажите, что из всех треугольников с данным основанием и данной высотой, проведенной к этому основанию, наименьший периметр имеет равнобедренный треугольник.
4. Внутри острого угла с вершиной О взяли точку А. Постройте на двух его сторонах точки В и С так, чтобы периметр треугольника АВС был наименьшим.
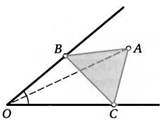
5. Найдите минимальный периметр треугольника АВС из предыдущей задачи, если ОА = 1, а величина данного угла равна 30°.
|
6. В треугольнике АВС боковые стороны АВ и ВС равны 1, а угол АВС равен 20°. На стороне АВ выбирают произвольную точку К, а на стороне ВС — произвольную точку Е. Найдите минимум |
|
|
суммы АЕ + ЕК 4- КС. |
|
|
В |
В А |
|
А |
А |
|
А |
|
|
А С |
А С |
|
К задаче 6 |
К задаче 7 |
7. Боковые стороны АВ и ВС равнобедренного треугольника АВС равны 1, а угол между ними равен 15°. На стороне АВ выбирают произвольную точку К, а на стороне ВС — произвольную точку Е. Найдите минимум АЕ 4- ЕК.
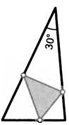
*8. Один из углов остроугольного треугольника равен 30°. На каждой его стороне выбрали по одной точке. Докажите, что минимальный периметр образованного этими точками треугольника равен одной из высот исходного треугольника.
*9. На каждой стороне прямоугольника взяли по одной точке. Докажите, что наименьший периметр образованного этими точками четырехугольника равен сумме диагоналей прямоугольника.
