Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Равнобедренный треугольник

![]()
основание
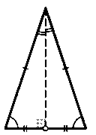
Треугольник называется равнобедренным, если у него есть две равные стороны. Эти равные стороны называют боковыми сторонами треугольника, а третью его сторону — основанием.
Медианой треугольника называется отрезок, соединяющий его вершину с серединой противоположной стороны.
Биссектрисой треугольника называется отрезок биссектрисы его угла от вершины до точки пересечения с противоположной стороной.
Высотой треугольника называется отрезок перпендикуляра, опущенного из его вершины на противоположную сторону, до точки пересечения с этой стороной (или ее продолжением).
Свойства равнобедренного треугольника
1. Два угла при основании равнобедренного треугольника равны.
2. Медиана, проведенная к основанию равнобедренного треугольника, совпадает с его высотой и биссектрисой
Признак равнобедренного треугольника Если в треугольнике два угла равны, то он равнобедренный.
1. Докажите, что биссектриса равнобедренного треугольника, проведенная к основанию, также является его медианой и высотой.
2. (Свойство равнобедренного треугольника.) Докажите, что у равнобедренного треугольника углы при основании равны.
3. Биссектриса данного треугольника одновременно является его высотой. Докажите, что данный треугольник равнобедренный.
4. На основании АС равнобедренного треугольника АВС взяли точки М и К так, что AM = СК. Докажите, что ВЫ = ВК.
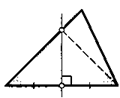
5. (Признак равнобедренного треугольника.) Два угла треугольника равны. Докажите, что он равнобедренный. Для доказательства воспользуйтесь приведенным здесь чертежом.
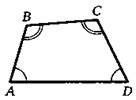
6. Дан четырехугольник ABCD, в котором ZA = ZD, ZB = ZC, причем прямые АВ и CD не параллельны. Докажите, что AB — CD.
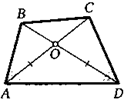
7. Диагонали четырехугольника ABCD пересекаются в точке О. Известно, что ZA = ZD, АО = OD. Докажите, что АВ = CD.
8. Дан четырехугольник ABCD, в котором АВ = ВС, AD = DC. Докажите, что его диагонали перпендикулярны.
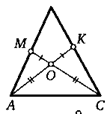
9. На сторонах АВ и ВС треугольника АВС взяли точки М и К. Отрезки АК и СМ пересекаются в точке О. Оказалось, что АО = СО, МО = КО. Докажите, что треугольник АВС равнобедренный.
В
10. (Существование перпендикуляра из точки на прямую.)
Докажите, что из любой точки, не лежащей на прямой, можно опустить на нее перпендикуляр.
11. Две стороны одного треугольника равны двум сторонам другого, а также равны их высоты, проведенные к третьим сторонам. Верно ли, что эти два треугольника равны?