Математические олимпиады по лигам. 5–9 классы - Андрей Николаевич Павлов 2007
Олимпиады по лигам (5-6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон
Высшая лига
1 тур
1. Найдите значение выражения (a ? a ? a — b ? b ? b): (а ? а + a ? b + b ? b), если а = 17, Ь = 14.
2. Решите уравнение 72: (38 ? 26: (17—92: х)) = 2.
3. Расставьте вместо букв цифры так, чтобы получилось верное равенство (разным буквам соответствуют разные цифры): У — Р = А: В = Н ? Е = Н + И = Е.
4. Из села по дороге в полдень вышла Таня со скоростью 6 км/ч. В 13 ч 00 мин вслед за ней вышел Игорь со скоростью 8 км/ч. А в 14 ч 00 мин из того же села вдогонку на велосипеде выехала Света. С какой скоростью должна ехать Света, чтобы догнать Игоря в тот момент, когда Игорь догонит Таню?
5. В команде 7 мальчиков и 6 девочек. Вначале все мальчики обменялись рукопожатиями друг с другом. Затем каждый мальчик обменялся рукопожатием с каждой девочкой. А вот девочки друг другу руки решили не жать. Сколько всего было рукопожатий?
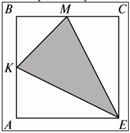
6. Дан квадрат АВСЕ со стороной 4 см. Точка К — середина стороны АВ, точка М — середина стороны ВС. Найдите площадь треугольника МКЕ.
2 тур
1. На могиле Диофанта (древнегреческий математик) имеется надпись: «Шестую часть его жизни заняло детство, двенадцатую — отрочество, седьмую — юность. Затем протекла половина его жизни, после чего он женился. Через 5 лет у него родился сын, а когда сыну минуло 4 года, Диофант скончался». Сколько лет жил Диофант?
2. Найдите х, если 54 км/ч = х м/с.
3. Алеша дал Боре столько яблок, сколько у Бори было. Потом Боря дал Алеше столько яблок, сколько у того стало. После этого у мальчиков оказалось по 4 яблока. Сколько яблок было у каждого первоначально?
4. Дядя Федор, кот Матроскин, Шарик и почтальон Печкин поспорили: кто больше выпьет молока. После того, как молоко было выпито, каждый из них высказался:
Дядя Федор: «А все-таки я не оказался последним!» Кот Матроскин: «Я выпил не больше, но и не меньше всех». Шарик: «Я маленький, поэтому выпил меньше всех». Почтальон Печкин: «Я вас всех победил!» Один из них сказал неправду. Кто победил в соревновании, и кто сказал неправду?
5. Вычислите 7288: 8 + 6363: 7 — 2000 + 1000: 250 + 276.
6. Частное равно 100. Делимое уменьшили на делитель. Узнайте новое частное.
3 тур
1. Найдите наибольшее целое число, дающее при делении на 13 неполное частное 17.
2. Сколько существует натуральных двузначных чисел, у которых первая цифра в два раза больше второй?
3. Найдите закономерность в последовательности чисел и определите, сколько в этой последовательности трехзначных чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
4. Три землекопа за 2 ч выкопали три ямы. Сколько ям выкопают шесть землекопов за 5 ч?
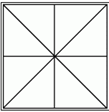
5. Сколько треугольников «спрятано» на рисунке?
6. Летела стая гусей, а навстречу им летит один гусь и говорит: «Здравствуйте, сто гусей!» А передний старый гусь ему и отвечает: «Нет, нас не сто гусей! Вот, если б нас было еще столько, да еще полстолька, да еще четверть столько, да ты, гусь, то было бы сто гусей, а теперь... Вот и рассчитай-ка, сколько нас?»
4 тур
1. 3 кедровых ореха можно обменять на 2 лимона, а 3 лимона можно обменять на 4 яблока. Сколько кедровых орехов можно обменять на 16 яблок?
2. Из цифр 0, 2, 3, 5, 8 составьте все трехзначные числа, сумма цифр в каждом из которых равна 8 (цифры в числе могут повторяться).
3. Путь, пройденный туристом за один день, оказался в три раза больше, чем половина оставшегося пути. Какую часть всего пути прошел турист за день?
4. Придумайте задачу, которая решалась бы с помощью уравнения 2 ? (х + 1) + х = 32.
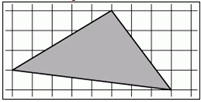
5. Найдите площадь треугольника, изображенного на рисунке. Площадь одной клетки равна 1.
6. В токарном цехе вытачиваются детали из стальных заготовок, из одной заготовки — деталь. Стружки, оставшиеся после обработки трех заготовок, можно переплавить и получить ровно одну заготовку. Сколько всего деталей можно сделать из 9-ти заготовок? А из 14-ти? Сколько нужно взять заготовок, чтобы получить 40 деталей?
5 тур
1. Сумма шести различных натуральных чисел равна 22. Найдите эти числа.
2. Пятиклассникам очень понравилась поездка в Великий Устюг, и они решили поехать туда снова, дабы навестить веселых Дедов Морозов. Ежемесячно каждый ученик вносил определенное количество рублей (без копеек), одинаковое для всех, и в течение пяти месяцев было собрано 49 685 р. Сколько было в группе учеников, и какую сумму внес каждый?
3. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «дамы» и никто не катается со своей сестрой. Самым высоким в компании был Юра Воробьев, следующим по росту — Андрей Егоров, потом Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Инна Крымоваи Аня Воробьева. Определите, кто с кем катался?
4. Простые числа имеют только два различных делителя — единицу и само это число. Найдите первые три числа, имеющие ровно три различных делителя. Догадаетесь ли вы, какие числа имеют только три различных делителя?
5. Полный бидон с молоком весит 34 кг, а наполненный до половины — 17 кг 500 г. Сколько весит пустой бидон?
6. Из литра молока получают 150 г сливок, а из литра сливок — 300 г масла. Сколько масла получится из 100 л молока?
6 тур
1. На почтовом ящике написано: «Выемка писем производится пять раз в день с 7 до 19 ч». И действительно, первый раз почтальон забирает почту в 7 ч утра, а последний — в 7 ч вечера. Через какие интервалы времени вынимают письма из ящика?
2. Вычислите 66 509 + 141 404: (39 839 — 39 793) + 1985.
3. В классе учится меньше чем 50 школьников. За контрольную работу седьмая часть учеников получила пятерки, третья — четверки, половина — тройки. Остальные работы были оценены как неудовлетворительные. Сколько всего учащихся в классе?
4. Ковбой Билл зашел в бар и попросил у бармена бутылку виски за 3 доллара и 6 коробков непромокаемых спичек, цену которых он не знал. Бармен потребовал с него 11 долларов 80 центов (1 доллар — 100 центов), и в ответ на это Билл вытащил револьвер. Тогда бармен пересчитал стоимость покупки и исправил ошибку. Как Билл догадался, что бармен пытался его обсчитать?
5. Однажды на лестнице была найдена странная тетрадь. В ней было записано четыре утверждения:
«В этой тетради ровно одно неверное утверждение»;
«В этой тетради ровно два неверных утверждения»;
«В этой тетради ровно три неверных утверждения»;
«В этой тетради ровно четыре неверных утверждения».
Есть ли среди этих утверждений верные, и если да, то какие?
6. Вася взял у товарища книгу на три дня. В первый день он прочел полкниги, во второй — треть оставшихся страниц, а в третий день прочитал половину прочитанного за первые два дня. Успел ли Вася прочитать всю книгу за три дня? Ответ обоснуйте.
7 тур
1. — Еще веревочку? — спросила мать, вытаскивая руки из лоханки с бельем. — Можно подумать, что я вся веревочная. Только и слышишь: веревочку да веревочку. Ведь я вчера дала тебе порядочный клубок. Куда ты ее девала?
— Во-первых, половину ты сама взяла обратно. Половину того, что осталось, взял у меня Том, чтобы удить в канаве колюшек. Осталось совсем немного, да из того еще папа взял половину для починки подтяжек, которые лопнули у него от смеха, когда случилась беда с автомобилем. А после понадобилось еще сестре взять две пятых оставшегося, чтобы завязать свои волосы узлом.
— Что же ты сделала с остальной веревочкой?
— С остальной? Остальной-то было всего-навсего 30 см! Вот и устраивай телефон из такого обрывка...
Какую же длину имела веревочка первоначально?
2. Ира, Наташа, Алеша и Витя собирали грибы. Наташа собрала больше всех, Ира не меньше всех, а Алеша — больше, чем Витя. Верно ли, что девочки собрали грибов больше, чем мальчики?
3. Чему равна площадь треугольника со сторонами 8, 7 и 15?
4. Пять первоклассников стояли в шеренгу и держали 37 флажков. У всех справа от Таты — 14 флажков, справа от Яши — 32, справа от Веры — 20, справа от Максима — 8. Сколько флажков у Даши?
5. Как при помощи чашечных весов без гирь разделить 24 кг гвоздей на две части — 9 и 15 кг?
6. Решите уравнение
![]()
8 тур
1. Шли три крестьянина и зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с картофелем на стол и ушла. Проснулся один крестьянин, увидел картофель и, чтобы не будить товарищей, сосчитал картофель, съел свою долю и снова заснул. Вскоре проснулся другой; ему невдомек было, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После него проснулся третий; полагая, что он проснулся первым, он сосчитал весь оставшийся в миске картофель и съел третью часть. Тут проснулись его товарищи и увидели, что в миске осталось 8 картофелин. Тогда только объяснилось дело. Сосчитайте, сколько картофелин подала на стол хозяйка?
2. Во время стоянки между двумя рейсами матросу исполнилось 20 лет. По этому случаю в кают-компании собрались все шесть членов команды.
— Я вдвое старше юнги и на 6 лет старше машиниста, — сказал рулевой.
— А я на столько же старше юнги, на сколько моложе машиниста, — заметил боцман. — Кроме того, я на 4 года старше матроса.
— Средний возраст команды — 28 лет, — дал справку капитан.
Сколько лет капитану?
3. В шахматном турнире участвовали 40 игроков, и каждый сыграл с каждым по одной партии. Сколько было сыграно партий?
4. Два пильщика должны распилить бревно, длина которого 5 1/2 м, на полуметровые чурки. Во сколько минут они сделают это, если распиловка бревна поперек продолжается каждый раз 2 1/2 мин?
5. В 100-значном числе 12345678901234567890...1234567890 вычеркнули все цифры, стоящие на нечетных местах; в полученном 50-значном числе вновь вычеркнули все цифры, стоящие на нечетных местах, и т. д. Вычеркивание продолжалось до тех пор, пока было что вычеркивать. Какая цифра была вычеркнута последней?
6. Докажите, что разность 9100— 7100делится на 10.
9 тур
1. На столе лежат в ряд четыре фигуры: треугольник, круг, прямоугольник и ромб. Они окрашены в разные цвета: красный, синий, желтый, зеленый. Известно, что красная фигура лежит где-то между синей и зеленой; непосредственно справа от желтой фигуры лежит ромб; круг лежит правее и треугольника, и ромба; треугольник лежит не с краю; синяя и желтая фигуры лежат не рядом. Определите, какого цвета какая фигура. Укажите все возможные решения.
2. Найдите значение выражения Зх3+ 2х2+ х, если
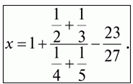
3. Два города, А и В, находятся на расстоянии 300 км друг от друга. Из этих городов одновременно выезжают друг другу навстречу два велосипедиста и мчатся, не останавливаясь, каждый со скоростью 50 км/ч. Но вместе с первым велосипедистом из города^ вылетает муха, пролетающая в час 120 км. Муха опережает первого велосипедиста, летит навстречу второму, выехавшему из В. Встретив его, она сразу поворачивает назад к велосипедисту А. Повстречав его, опять летит обратно навстречу велосипедисту В, и так продолжает она свои полеты взад и вперед до тех пор, пока велосипедисты не съехались. Тогда она успокоилась и села одному из велосипедистов на шапку. Сколько километров пролетела муха?
4. Школьник сказал своему приятелю Вите:
— У нас в классе семнадцать человек. И, представь, каждый из них дружит ровно с пятью одноклассниками.
— Не может этого быть, — сразу ответил Витя.
Почему он так решил?
5. Женю, Леву и Гришу рассадили так, что Женя мог видеть Леву и Гришу, Лева-только Гришу, а Гриша — никого. Потом из мешка, в котором лежали две белые и три черные шапки (содержимое мешка было известно мальчикам), достали и надели на каждого шапку неизвестного ему цвета, а две шапки остались в мешке (какие именно — мальчикам неизвестно).
Женя сказал, что он не может определить цвет своей шапки. Лева слышал ответ Жени и сказал, что и у него не хватает данных для определения цвета своей шапки. Мог ли Гриша на основании этих ответов определить цвет своей шапки? Если нет, то почему; если да, то как?
6. «То» да «это», да половина «того» да «этого» — сколько это будет процентов от трех четвертей «того» да «этого»?
10 тур
1. На экзамене преподаватель предлагает студенту пять вопросов, на которые надо ответить «да» или «нет». Студент знает, что ответов «да» больше, чем «нет», и что преподаватель никогда не задает три вопроса подряд, требующие одинакового ответа. Из содержания первого и последнего вопросов ему ясно, что ответы на них должны быть противоположны. Единственный вопрос, ответ на который ему известен, — второй. И этот ответ — «нет». Какими должны быть ответы на эти пять вопросов?
2. В меню входят: овощной суп или бульон на первое, бифштекс, цыпленок или рыба на второе и компот или мороженое на третье. Полный обед состоит из одного блюда на первое, одного блюда на второе и одного блюда на третье.
а) Сколько может быть различных полных обедов?
б) Сколько может быть полных обедов с бифштексом в качестве второго?
3. Имеется девять монет, о которых известно, что восемь из них имеют одинаковый вес, а девятая несколько тяжелее остальных. Покажите, что более тяжелая монета может быть отделена от остальных посредством двух взвешиваний на чашечных весах (без гирь).
4. Изготовление книги включает в себя несколько стадий: сначала ее набирают, затем печатают и наконец делают к ней обложку и переплетают. Допустим, что наборщик берет 6 долларов (600 центов) в час, бумага стоит 1/4 цента за лист, печатник берет 11 центов за каждую минуту работы его пресса, обложка стоит 28 центов и переплетчик берет 15 центов за переплетение каждой книги. Допустим теперь, что издатель хочет напечатать книгу, для которой требуется 300 ч работы наборщика, 220 листов бумаги на один экземпляр и 5 мин работы одного печатного пресса на каждый экземпляр. Найдите стоимость издания одного экземпляра книги.
5. Что больше и на сколько: 20 % от 30 или 30 % от 20?
6. Маша съедает коробку конфет за 5 мин, а Даша — за 6 мин. За какое время будут съедены все конфеты, если Маша и Даша займутся решением данного вопроса одновременно?