Математические олимпиады по лигам. 5–9 классы - Андрей Николаевич Павлов 2007

Олимпиады по лигам (5-6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон
Первая лига

1 тур

1. Вычислите 828 828: 138 — 5644.

2. Найдите значение выражения (х + у ? z): t — f, если х = 450 044, у = 203, z =470, t =6, f = 999.

3. Подберите такое натуральное число х, чтобы х ? х + х = 992.

4. Запишите самое большое трехзначное число, сумма цифр которого равна 15.

5. Точки А, В, С, лежат на одной прямой. Длина отрезка АВ равна 6 см, длина отрезка ВС равна 8 см. Чему может равняться длина отрезка АС?

6. Скорость катера по течению 48 км/ч, а против течения 40 км/ч. Чему равна скорость течения?

2 тур

1. Вычислите 809 ? 43—97 + 13 662 000: 27 000.

2. Найдите значение выражения х + 6 + 5х — 4 — 2х + 3 — 4х, если х = 307.

3. Восстановите запись: * 8 ? * = 8**. Укажите все решения.

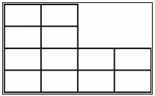
4. Сколько прямоугольников, считая большой, «спрятано» на рисунке?

5. Если бы Аня купила 3 тетради, то у нее осталось бы 5 р., а если бы Аня купила 4 тетради, то ей не хватило бы 5 р. Сколько денег было у Ани?

6. Найдите наименьшее натуральное пятизначное число, которое делится на 9, и чтобы первая цифра была 7 и все цифры различны.

3 тур

1. Вычислите 35 ? 202 — 51 948: (1577 — 44 ? 35) + 334.

2. Нарисуйте отрезок АВ длиной 4 см. Отметьте середину отрезка-точку С. Отметьте точку D — середину отрезка АС. На луче DC отметьте точку Е так, чтобы длина отрезка DE была равна 7 см. Чему равно расстояние от В до Е?

3. Разрежьте фигуру, изображенную на рисунке, на 4 одинаковые части.

4. Турист прошел половину пути, затем треть оставшегося пути, после чего ему осталось пройти 6 км. Чему равен весь путь туриста?

5. Мастер за 8 ч делает 80 деталей, а его ученик за 5 ч делает 25 деталей. За сколько часов они изготовят 45 деталей, если будут работать вместе?

6. В мастерской по пошиву одежды от куска сукна в 200 см ежедневно, начиная с 1 декабря, отрезали по 2 дм. Когда был отрезан последний кусок?

4 тур

1. Решите уравнение 18 408: (268 ? 75—19 746) — х = 42.

2. В этом примере умножения больше половины цифр заменено звездочками. Восстановите недостающие цифры:

3. Какой угол составляют между собой часовая и минутная стрелки часов в 16 ч?

4. Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 2 раза меньше?

5. На уроке физкультуры ученики выстроились в линейку на расстоянии 1 м друг от друга. Вся линейка растянулась на 21 м. Сколько было учеников?

6. В школе 368 учащихся. Докажите, что среди учащихся этой школы обязательно найдутся хотя бы два ученика, отмечающие свой день рождения в один и тот же день.

5 тур

1. Вычислите 66 509 + 141 404: (39 839 — 39 793) + 1985.

2. Решите уравнение 12х + 4 — 5х + 21 = 8x.

3. На какую цифру оканчивается число 42004(произведение 2004 четверок)?

4. 2/5 числа равны 12. Найдите: а) само число; б) 60 % этого числа.

5. Найдите длину стороны квадрата, если его площадь численно равна периметру.

6. Сейчас Сереже 11 лет, а Вове 1 год. Сколько лет будет Сереже и Вове, когда Сережа станет втрое старше Вовы?

6 тур

1. Вычислите (2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8 ? 9): (1 2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8).

2. Подберите число n так, чтобы уравнение nx + 1 = х не имело решений.

3. Мачеха, уезжая на бал, дала Золушке мешок, в котором были перемешаны мак и просо, и велела перебрать их. Когда Золушка уезжала на бал, она оставила три мешка: в одном было просо, в другом — мак, а в третьем — еще не разобранная смесь. Чтобы не перепутать мешки, Золушка к каждому из них прикрепила по табличке: «Мак», «Просо» и «Смесь».

Мачеха вернулась с бала первой и нарочно поменяла местами таблички так, чтобы на каждом мешке оказалась неправильная надпись. Ученик Феи успел предупредить Золушку, что теперь ни одна надпись на мешках не соответствует действительности. Тогда Золушка достала только одно-единственное зернышко из одного мешка и, посмотрев на него, сразу догадалась, где что лежит. Как она это сделала?

4. Кувшин = бутылка + стакан; два кувшина = семь стаканов; бутылка = чашка + два стакана; бутылка = сколько чашек?

5. В кабинете со звуконепроницаемыми стенами висят настенные часы, которые бьют каждые полчаса (один удар) и каждый час (столько ударов, сколько показывает часовая стрелка). Однажды, открыв дверь в кабинет, хозяин услышал один удар часов. После этого хозяин не уходил из кабинета. Через полчаса часы в кабинете пробили еще раз — опять один удар. Спустя полчаса — еще один удар. Наконец, еще через полчаса часы снова пробили один раз. Какое время показывали часы, когда хозяин входил в кабинет?

6. В соревновании участвовали 50 стрелков. Первый выбил 60 очков; второй — 80; третий — среднее арифметическое очков первых двух; четвертый — среднее арифметическое очков первых трех. Каждый следующий выбил среднее арифметическое очков всех предыдущих. Сколько очков выбил 50-й стрелок?

7 тур

1. Вычислите 612 228 + (53 007 — 52 275: 615).

2. Подберите такое натуральное число х, чтобы х(х + 1)(х + 2) = 720.

3. Сколько раз в течение суток часовая и минутная стрелки составляют прямой угол?

4. Найдите двузначное число, которое в семь раз больше цифры его единиц.

5. Тане не хватало 7 р., а Гале — 2 р., чтобы купить по коробке цветных карандашей. Когда они сложили свои деньги, их не хватило даже на покупку одной коробки. Сколько стоит коробка карандашей?

6. Собака погналась за лисицей, которая была на расстоянии 30 м от нее. Скачок собаки равен 2 м, скачок лисицы 1 м. В то время как лисица делает 3 скачка, собака делает 2 скачка. Какое расстояние должна пробежать собака, чтобы догнать лисицу?

8 тур

1. Напишите наименьшее натуральное число, составленное из всех цифр, которое делится на 5.

2. Один из пяти братьев испек маме пирог. Никита сказал: «Это Глеб или Игорь». Глеб сказал: «Это сделал не я и не Дима». Игорь сказал: «Вы оба шутите». Андрей сказал: «Нет, один из них сказал правду, а другой обманул». Дима сказал: «Нет, Андрей, ты не прав». Мама знает, что трое из ее сыновей всегда говорят правду. Кто испек пирог?

3. Известно, что в январе четыре пятницы и четыре понедельника. На какой день недели приходится 1 января?

4. Расставьте 24 человека в 6 рядов так, чтобы каждый ряд состоял из 5 человек.

5. Эта старинная задача была известна еще в Древнем Риме. Богатый сенатор, умирая, оставил жену в ожидании ребенка. После смерти сенатора выяснилось, что на свое имущество, равное 210 талантам, он составил следующее завещание: «В случае рождения сына отдать мальчику две трети состояния (то есть 140 талантов), а остальную треть (то есть 70 талантов) — матери; в случае же рождения дочери отдать девочке одну треть состояния (то есть 70 талантов), а остальные две трети (то есть 140 талантов) — матери».

У вдовы сенатора родились близнецы — мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наибольшим приближением к условию завещания?

6. Решите уравнение (х — 2)/3 + 2 = 4.

9 тур

1. Вычислите

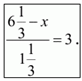
2. Решите уравнение

3. Припишите к числу 10 справа и слева одну и ту же цифру так, чтобы полученное четырехзначное число делилось на 12.

4. Гена пошел с папой в тир. Договорились, что Гена делает 5 выстрелов и за каждое попадание в цель получает право сделать еще 2 выстрела. Всего Гена сделал 17 выстрелов. Сколько раз он попал в цель?

5. Как-то в минуту отдыха друзья-мушкетеры — Атос, Портос, Арамис и дАртаньян решили померяться силой при перетягивании каната. Портос с д Артаньяном легко перетянули Атоса с Арамисом. Но когда Портос встал в паре с Атосом, то победа против Арамиса с дАртаньяном досталась им уже не так легко. Когда же Портос с Арамисом оказались против Атоса с дАртаньяном, то ни одна из этих пар не смогла одолеть друг друга. Можете ли вы определить, как мушкетеры распределяются по силе?

6. Ваня и Вася — братья-близнецы. Один из них всегда говорит правду, а другой всегда лжет. Вы можете задать только один вопрос одному из братьев, на который он ответит «да» или «нет». Попробуйте выяснить, как зовут каждого из близнецов.

10 тур

1. Угол в 12 3/4 градуса рассматривают в лупу, дающую четырехкратное увеличение. Какой величины покажется угол?

2. В дремучем Муромском лесу из-под земли бьют два источника мертвой воды: № 1 и № 2. Из источника № 1 мертвую воду может взять каждый, а источник № 2 находится в пещере Кощея, в которую никто, кроме самого Кощея, попасть не может.

На вкус и цвет мертвая вода ничем не отличается от обыкновенной, однако если человек выпьет из какого-нибудь источника, он через сутки умрет. Правда, если он выпьет из источника № 1, спасти его может только одно: если он в течение суток выпьет яд из источника № 2. А если он сразу выпьет яд из источника № 2, то ему уже ничто не поможет.

Иванушка-дурачок вызвал Кощея на дуэль. Условия дуэли были такие: каждый приносит с собой кружку с жидкостью и дает ее выпить своему противнику. Кощей обрадовался: «Ура! Я дам яд № 2, и Иванушка-дурачок не сможет спастись! А сам выпью яд из источника № 1, который Иванушка-дурачок мне принесет, затем выпью свой яд № 2 и спасусь!»

В назначенный день оба противника встретились в условленном месте. Они честно обменялись кружками и выпили то, что в них было. Каковы же были радость и удивление обитателей Муромского леса, когда оказалось, что Кощей умер, а Иванушка-дурачок остался жив! Догадайтесь, как?

3. На волшебной яблоне выросли 15 бананов и 20 апельсинов. Если сорвать один из плодов — вырастет такой же, если одновременно сорвать два одинаковых плода — вырастет апельсин, а если одновременно сорвать два разных плода — вырастет банан. Ася срывала плоды, и в конце концов на яблоне остался ровно один плод. Можете ли вы определить, какой это был плод?

4. Мальчик плотно прижал грань синего карандаша к грани желтого карандаша. Один сантиметр (в длину) прижатой грани синего карандаша, считая от нижнего конца, запачкан краской. Желтый карандаш мальчик держит неподвижно, а синий, продолжая прижимать к желтому, опускает на 1 см, затем возвращает в прежнее положение, опять опускает на 1 см и опять возвращает в прежнее положение; 3 раза он так опускает и 3 раза поднимает синий карандаш (6 движений). Допустим, что за это время краска не высыхает и не истощается. На сколько сантиметров в длину окажется запачканным желтый карандаш после шестого движения?

5. Решите задачу из немецкого рукописного трактата из мюнхенского собрания (XV век).

«Некто имеет работников и деньги. Если он даст каждому работнику 5 монет, у него остается 30, а если 7 монет, то не хватит 30. Спрашивается, сколько у него работников?»

6. Решите уравнение