Геометрические тела и их изображение - Геометрические тела и их изображение - Многогранники

Цели: закрепить представление о многограннике и его элементах, познакомить учащихся со способами изображения пространственных тел.

Ход урока

I. Организационный момент.

II. Актуализация знаний.

1. Фронтальная работа с классом.

На плакате изображены геометрические тела. Укажите среди них:

а) пирамиды, конусы, цилиндр, шар, призмы;

б) тела, не являющиеся многогранниками;

в) многогранник, у которого 5 граней, 5 вершин и 8 ребер;

г) 2 различных многогранника с одинаковым числом граней.

2. Тест.

1). Если у прямоугольного параллелепипеда закрасить одним цветом параллельные ребра, то сколько цветов потребуется?

К — 2 И — 6 Э — 3

2). Сколько граней у неотточенного шестигранного карандаша?

А — 6Й — 8Р — 10

3). Дана призма, основанием которой является восьмиугольник. Сколько у этой призмы вершин?

Л — 16 В — 18 У — 9

4). Сколько потребуется проволоки для изготовления каркасной модели шестиугольной пирамиды, все ребра которой равны 5 см?

М — 30 Е — 60 Б — 80

5). Какая из фигур, изображенных на рисунке 186, является разверткой куба? Заполнив бланк ответов, вы прочитаете фамилию одного из величайших математиков.

1	2	3	4	5
Э	Й	Л	Е	Р

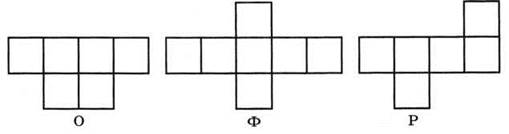
Рис. 186

3. Краткая справка об ученом Леонарде Эйлере.

Леонард Эйлер — один из величайших математиков XVIII в. Этот гениальный ученый, родившийся в Швейцарии, почти всю жизнь прожил в России, и мы считаем его своим соотечественником.

Труды Эйлера поражают своим объемом и разносторонностью. Полное собрание сочинений ученого занимает 72 тома. Это работы по математике, астрономии, кораблестроению, артиллерии и даже по теории музыки.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения, но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он не писал сам, а диктовал своим ученикам.

Несколько математических формул носят имя Эйлера. Имя Эйлера носит формула, связывающая число вершин, ребер и граней выпуклого многогранника.

В - Р + Г = 2

III. Формирование умений и навыков.

1. Проверка и обсуждение домашней работы из РТ, часть 2, № 112 (г).

2. У, № 1105.

3. Практическая работа. РТ, часть 2, № 110, 114. Самопроверка (ученик из предложенных моделей выбирает ответы (а), (б), (в) и прикрепляет их к плакату на доске, объясняя свой выбор. Учащиеся проверяют свою работу).

4. Самостоятельная работа. РТ, часть 2, № 113, 115.

IV. Итоги урока.

1. Как изображаются на чертеже невидимые ребра многогранников? видимые ребра многогранников?

2. Как расположены видимые и невидимые грани?

V. Домашнее задание.

У, п. 10.1, № 1108, 1111, 1113.