Путешествие в историю математики - Свечников А. А. 1995
Как быстрее вычислять?
Абак и счеты
Долгое время счет для людей оставался трудным занятием. Значительно легче было считать на пальцах рук и ног, которые стали как бы первой счетной машиной. Постепенно люди придумали немало хитроумных способов счета при помощи не только пальцев, но и суставов. Однако так можно было выполнять некоторые действия лишь с небольшими числами. С развитием хозяйственной деятельности человек стал оперировать большими числами, используя однородные предметы: камешки, ракушки, орехи, бобы и т. п. Для удобства подсчета в употребление вошли специальные доски, на которых раскладывали эти предметы и пересчитывали их.
Со временем доски для подсчета стали расчерчивать на несколько полос или колонок. Это позволило вести счет с помощью однородных предметов значительно быстрее. Например, чтобы сложить числа 231 и 156, не надо было брать такое же количество предметов. Достаточно было положить в первую колонку 1 предмет, во вторую — 3, в третью — 2. Затем в таком же порядке под этими предметами раскладывали число 156. Подсчитав число предметов в каждой отдельной колонке (в первой их было 1 + 6 = 7, во второй 3 + 5 = 8, в третьей 2 + 1 = 3), можно было определить сумму 387.
Так люди пришли к изобретению абака — счетной доски, которая многие сотни лет в разных странах помогала экономить время в действиях с большими числами.
Абак за время своего существования постепенно совершенствовался. Первоначально это была доска, посыпанная тонким слоем мелкого песка или порошком из голубой глины. На ней простой палочкой можно было писать буквы, числовые знаки, чертить фигуры, а при необходимости все это стирать. Такой доской обычно пользовались при обучении. От порошка, покрывающего доску, вероятно, и произошло само название абак. Это слово имеет корень -бак, что в переводе с древнееврейского языка на русский означает «песок, прах, пыль».

Для практических подсчетов абак расчерчивали линиями на полосы или колонки. Впоследствии колонки вверху дужками объединяли в группы по три. Каждая такая группа представляла собой определенный класс (числовой). Такое усовершенствование позволяло быстрее прочитывать числа, выложенные на абаке.
Предполагают, что древние вавилоняне пользовались абаком с колонками, соответствующими шестидесятеричной системе счисления.
Имеется упоминание о том, что в Греции абак существовал уже в V в. до н. э. На древней вазе сохранилось изображение грека, считающего на абаке. Археологи прошлого века при раскопках нашли старинный абак. Он имеет вид мраморной плиты размером 105 см х 75 см с высеченными на ней линиями.
При дальнейшем усовершенствовании абака стали пользоваться специально изготовленными кружками или квадратиками — жетонами. Позже (в I в. до н. э.) вошли в употребление «меченые жетоны», т. е. кружки или квадратики с проставленными на них цифрами (метками). Такие жетоны называли апексами.
Древние римляне пользовались абаком в виде доски или особого столика, крышка которого была разделена на полосы или колонки. Вверху каждой колонки стояли знаки, указывающие разряд чисел — единицы, десятки, сотни и т. д.
Старинный абак и древние счеты.

Пользовались, хотя сравнительно недолго, абаком и народы Индии. Десятичное позиционное счисление и нумерация, разработанные в Индии, позволяли выполнять действия письменно. Свои вычисления индийцы делали на песке, поэтому они отказались от абака, расчерченного на колонки, а пользовались простой доской, покрытой слоем песка. На таком приборе было удобно не только записывать числа, но и без труда заменять одну цифру другой, если это требовалось при вычислениях.
Арабы, переняв абак у индийцев и переселившись на запад после завоевания Испании (VIII в.), продолжали считать на абаке значительно дольше индийцев. От западных арабов (начиная с X в.) абак переняли народы Европы.
Абак, а точнее его близкий собрат — счетная скамья, которая на нескольких языках (немецкий, итальянский и др.) называется «банка», дала повод назвать учреждение, в котором производят разнообразные денежные операции, словом банк.
В Древней Руси при счете также применяли приборы, близкие к абаку. Первоначально они, по-видимому, были позаимствованы у римлян или греков, но впоследствии усовершенствованы на свой лад. О том, что у нас считали на абаке, говорит крылатое выражение «остался на бобах». Надо полагать, это выражение сложилось при игре, когда выигрыш и проигрыш подсчитывался на абаке с помощью бобов. Тот, кто, проиграв, отдавал все свои деньги, оставался только с бобами, на которых считал, т. е. «оставался на бобах».
Считая на абаке, числа нередко откладывали особыми костями. Такой способ у нас называли «счет костьми». Несколько позже на Руси получил широкое распространение «дощаный счет». Этот прибор состоял из ряда шнуров с нанизанными на них косточками. Впоследствии этот прибор стали делать в виде рамы с рядом стержней, на каждом из которых был нанизан десяток костей. В XVI в. этот прибор уже имел вид русских счетов, которые были значительно совершеннее абака и поэтому употребляются и в наши дни.
Русские счеты после войны с Францией (1812) были завезены пленными во Францию и получили распространение в Европе.
Своеобразные приборы, похожие на наши счеты, но более сложные, применялись с давних пор в Китае и Японии.
Счет на линиях
Европейские математики в XIII в. разработали счет на линиях, позаимствовав приемы счета на абаке.
На листе бумаги, разделенном на две части, проводили несколько параллельных отрезков с промежутками в 2 — 5 см. Число откладывали с помощью кружков или жетонов, пользуясь пятеричной системой счисления. Жетон, расположенный на нижней линии, означал 1, а жетон, лежащий между первой и второй линиями, означал 5. Жетон на второй линии означал 10, а жетон, лежащий выше этой линии, — 50. На третьей линии жетон означал 100.
Жетон, положенный выше третьей линии, но ниже четвертой, уже означал 500 и т. д. На рис. показано, как отложить на линиях число 367.
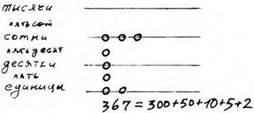
На одной половине листа выкладывали первое число, а на другой — второе. Выполняя сложение, складывали жетоны, расположенные на одном отрезке или в одном и том же промежутке между линиями. Результат сложения записывали или выкладывали также на линиях в нижней части листа. В Западной Европе лишь в XVI в. счет на линиях стал вытесняться «счетом пером» — письменными вычислениями.
Абацисты и алгоритмики.
Старинная гравюра.

Борьба между абакистами и алгоритмиками
Утверждение десятичной позиционной системы счисления и нумерации происходило в борьбе нового со старым. Новая система медленно распространялась в Европе в течение XII и XIII вв. До этого времени в Западной Европе действия с числами выполняли только с помощью абака, устно или на линиях. Знакомство с десятичной позиционной системой счисления и нумерацией привело к тому, что некоторые математики стали отказываться от применения абака и перешли к письменным вычислениям — к счету пером (так называли этот способ вычислений в то время).
Сторонники абака (абакисты) стремились сохранить укоренившийся способ математических вычислений. Новый способ — счет пером — для них был непривычен. Им было трудно и сложно переучиваться. Абакисты отвергали счет пером. Они уверяли, что только абак позволяет считать быстро, легко и безошибочно.
Сторонников письменных вычислений прозвали алгоритмиками. Они упорно боролись за нововведение. Сторонники нового — алгоритмики утверждали, что счет пером проще, удобнее и его легко проверить, дабы устранить ошибки.

Между абакистами и алгоритмиками во многих городах проходили своеобразные турниры-диспуты о преимуществах того или иного способа вычислений. Диспуты сопровождались практическими вычислениями на скорость — кто скорее и без ошибок произведет одни и те же вычисления на абаке или пером. Довольно часто эти турниры перерастали в жаркие споры, а иногда заканчивались крупными скандалами.
Борьба старого и нового нашла свое отражение в ряде рисунков. Победе алгоритмиков способствовали работы ученых Средней Азии, и особенно аль-Хорезми, имя которого послужило возникновению термина алгоритм. Значительную роль в победе алгоритмиков сыграла практическая потребность в быстром и удобном счете.
Заключительный удар по аба- кистам нанес первый ученый-математик Европы Леонардо Пизанский — Фибоначчи. Он родился в конце XII в. в семье купца и еще мальчиком научился производить вычисления на абаке. Позднее в путешествиях по Египту, Сирии, Греции и другим странам он познакомился с различными способами вычислений и пришел к выводу, что индусский способ — наилучший. Большое влияние оказали на него арабские математики.

В 1202 г. Фибоначчи написал и издал «Книгу абака». Она начинается так: «Девять индусских знаков суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски «сифр», можно написать какое угодно число». В этой книге изложены основы математических знаний того времени.
«Книга абака» разрушила все доводы абакистов в пользу счета на абаке. Запись чисел с употреблением нуля, о чем писал Фибоначчи, позволяла производить любые вычисления письменно значительно проще и быстрее, чем на абаке. Хотя «Книга абака» была сложна для понимания, сведения из нее постепенно распространялись и нашли практическое применение. Торговые люди того времени, которые больше других нуждались в скорых и правильных вычислениях, увидели в счете пером удобный и быстрый способ всевозможных расчетов.

Репутация Фибоначчи как вычислителя привлекла внимание даже правителя Священной Римской империи Фридриха II (1194 — 1250). Однажды Фридрих во главе большой свиты посетил город Пизу, чтобы лично убедиться в искусстве знаменитого вычислителя. В честь знатных гостей в городе был устроен большой математический турнир, на котором Фибоначчи быстро решил несколько сложных задач, обнаружив блестящий талант математика и вычислителя.
Изображение училища из букваря 1701 г.

Купцы, участвующие в оживленной торговле со странами Востока, высоко оценили преимущества подсчета, которым пользовались арабы и который распространяли алгоритмики. В городах объединения купцов стали подыскивать мастеров, знающих новые индо-арабские приемы вычислений, и нанимали их для обучения своих детей и торговых людей. Именно эти мастера-алгоритмики — учителя математики и содействовали широкому распространению счета пером.
Пользовались услугами счетных мастеров и в некоторых прибалтийских городах, а позднее, в XVIII в., и в Москве была открыта Математико-навигацкая школа. По ее образцу в ряде городов России были созданы так называемые цифирные школы, в которых особое внимание уделялось изучению математики и географии. В цифирных школах преподавали бывшие ученики навигацкой школы. Цифирные школы сыграли большую роль в распространении математических знаний и культуры в нашей стране.
Упражнения и задачи
1. Произведите вычисления на счетах с «волшебным числом» 142 857, которое дает следующие результаты:
142 857 • 2 = 285 714
142 857 • 3 = 428 571
142 857 • 4 = 571 428
142 857 • 5 = 714 285
142 857 • 6 = 857 142
142 857 • 7 = 999 999
Примечание. При умножении на 2, 3, 4, 5, 6 в произведениях получаются числа, состоящие из цифр данного числа, а при умножении на 7 в произведении окажутся только девятки. Проверьте!
2. Умножьте число 3367 на 33, 66, 99, 132... 264, 297. В произведениях получим: 111 111, 222 222, 333 333... 888 888, 999 999.
Геометрия — это наука хорошо измерять.
П. Рамус
