Путешествие в историю математики - Свечников А. А. 1995

Таблица умножения

«Пятью пять — двадцать пять, шестью шесть — тридцать шесть». Все школьники помнят эти две строки из таблицы умно­жения. Но не каждый учащийся знает, когда и в каком виде она появилась.

Еще в глубокой древности мно­гие математики, чтобы облегчить труд, пользовались таблицами для умножения и деления чисел. Однако вавилонские, египетские,

греческие и даже римские табли­цы до нас не дошли. Самая ранняя таблица умножения (I в.), дошед­шая до нас, по своей форме близ­ка к известной нам так называе­мой пифагоровой таблице умно­жения, записанной в квадрате, состоящем из 100 клеток. В ней все произведения чисел от 1 до 10 повторяются дважды.

В книге, изданной в 1496 г., по­добная таблица случайно была названа пифагоровой, хотя ника­кого отношения к Пифагору¹ она не имеет. Все же это название за квадратной таблицей умножения сохранилось и дошло до наших дней.

¹ Древнегреческий философ и матема­тик Пифагор жил в VI в. до н. э.

Такой вид имела усовершенствованная в XV в. таблица умножения.

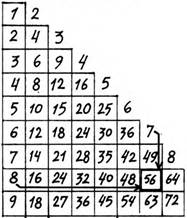
Недостатком квадратной таб­лицы умножения является нерациональное повторение произве­дений: например, в ней записано 4 • 5 и 5 • 4. Запоминание таблицы умножения требовало много вре­мени. Поэтому еще в XII в. были созданы треугольные таблицы умножения, в которых одно и то же произведение записано толь­ко один раз. Вот какой вид имела усовершенствованная в XV в. таб­лица умножения.

По этой таблице произведение 7•8 будет соответствовать числу, стоящему в седьмом столбце восьмой строки (цифры над ка­ждым столбцом указывают и но­мер столбцов).

Математик аль-Хорезми реко­мендовал таблицу умножения за­учить наизусть: «И если ты захо­чешь умножить какое-нибудь чи­сло на другое с помощью индий­ских букв (цифр), необходимо за­помнить умножение чисел, кото­рые имеются между единицей и девятью, друг на друга, совпада­ют ли эти числа или они различ­ны».

В Москве в 1682 г. была напеча­тана книга «Считание удобное, которым всякий человек купа­ющий и продающий зело удобно изыскати может число всякие ве­щи». В ней приведены таблицы произведений всех целых чисел от 1 до 100. В пояснении дано опи­сание, как пользоваться данной таблицей. Применяя эту таблицу, без особого труда можно опреде­лить, например, произведение 37 • 26 и др.

В XVIII в. в «Арифметике» Л. Ф. Магницкого таблица умно­жения дана в рациональном ви­де. Вот отдельные столбцы из нее:

Каждый следующий столбик уменьшается на одну строку, и по­следний из них имеет вид:

Автор наказывал: «Таблицу на­до заучить и всегда ее помнить, а если кто ее забудет, то пользы не будет».

Упражнения и задачи

1. Выполнить действия и проверить де­вяткой: 3729 + 12 068; 863 • 647

2. Произвести умножение решеткой: 1829 • 367; 468 • 248

3. Произвести умножение по методу академика А. Н. Крылова: 6274 • 845

4. Какой цифрой оканчивается сумма: 21 • 34 • 46 + 64 • 29 • 37?