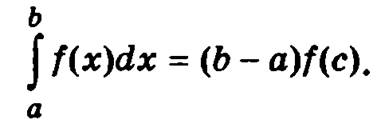Высшая математика мини-справочник для ВУЗов
Свойства определенного интеграла - ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пусть функция f(x) определена на отрезке [а, b]. Разобьем данный отрезок произвольным образом точками x0, x1, х2, ..., xn-1, хn такими, что
а = х0 < x1 < х2 < ...< xn-1 < xn = b,
на отрезки [хi, xi+1], где i = 0, 1, 2, ..., n - 1.
На каждом из полученных отрезков произвольным образом выберем точку τi ∈ [хi, xi+1], вычислим значение функции в этих точках f(τi) и построим интегральную сумму 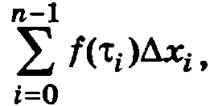 где ∆xi = xi+1 – xi.
где ∆xi = xi+1 – xi.
Обозначим через λ длину наибольшего из отрезков [хi, xi+1]: 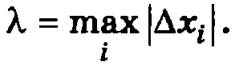
Если существует конечный предел интегральных сумм 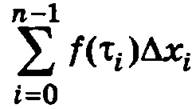 при λ → 0 (когда осуществляется переход к более мелкому разбиению отрезка [а, b], при котором длина наибольшего из полученных в результате разбиения отрезков стремится к нулю), то этот предел называется определенным интегралом функции f(x) по отрезку [а, b]
при λ → 0 (когда осуществляется переход к более мелкому разбиению отрезка [а, b], при котором длина наибольшего из полученных в результате разбиения отрезков стремится к нулю), то этот предел называется определенным интегралом функции f(x) по отрезку [а, b]
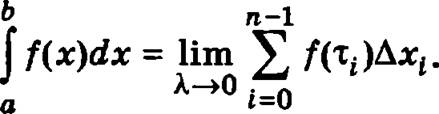
При этом а называется нижним пределом, а b — верхним пределом интегрирования.
Если существует указанный предел, то есть определенный интеграл, то функция f(x) называется интегрируемой на отрезке [а, b].
7.1. Свойства определенного интеграла
1. Постоянный множитель можно выносить за знак определенного интеграла:
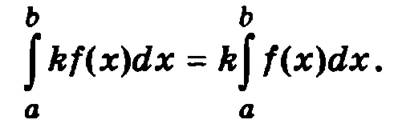
2. Определенный интеграл от конечной алгебраической суммы функций равен такой же сумме определенных интегралов от этих функций:
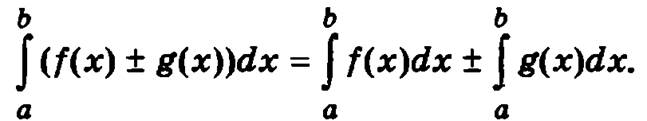
3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный:
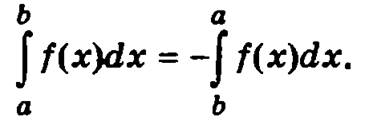
4. Если верхний предел интегрирования равен нижнему пределу, то определенный интеграл равен нулю:
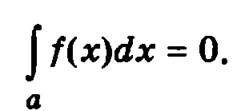
5. Если функция f(x) интегрируема на отрезках [а, с] и [с, b], то она будет интегрируемой и на отрезке [а, b] и
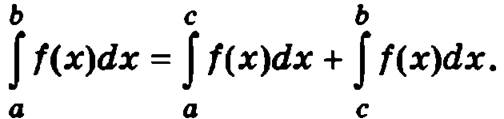
6. Если функция f(x) интегрируема на отрезке [а, b] и m ≤ f(x) ≤ М на этом отрезке, то справедливо неравенство
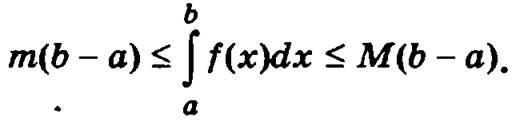
7. Если f(x) непрерывна на отрезке [а, b], то су шествует такая точка с, принадлежащая отрезку [а, b], что