Основные методы вычисления интегралов - НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Метод непосредственного интегрирования

Метод непосредственного интегрирования заключается в том, что, применяя тождественные преобразования подынтегрального выражения, исходный интеграл, используя свойство линейности

сводится к нескольким более простым, которые могут быть вычислены непосредственно по таблице интегралов.

Пример.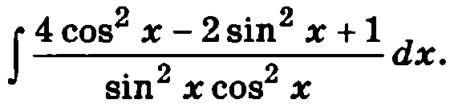

Применяя основное тригонометрическое тождество sin2 х + cos2 х = 1, получим

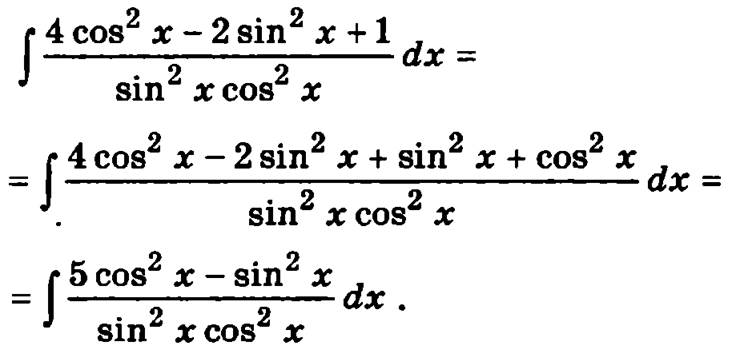
Разделим каждое слагаемое числителя в подынтегральном выражении на знаменатель:

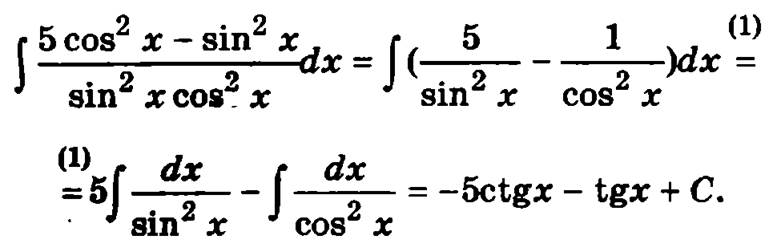
Метод интегрирования по частям

При использовании метода интегрирования по частям предполагается, что подынтегральное выражение может быть представлено в виде произведения некоторой функции и на дифференциал другой функции dv: ∫ udv.

Тогда, используя формулу интегрирования по частям

исходный интеграл заменяется другим ∫ vdu, который часто бывает более простым для вычисления.

Пример. ∫ x(3 sin x - 5 cos x)d.

Выберем в качестве u = х. тогда

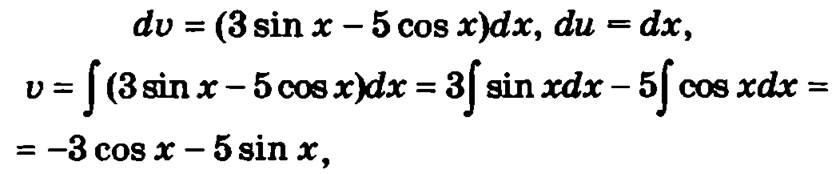
и по приведенной выше формуле получим

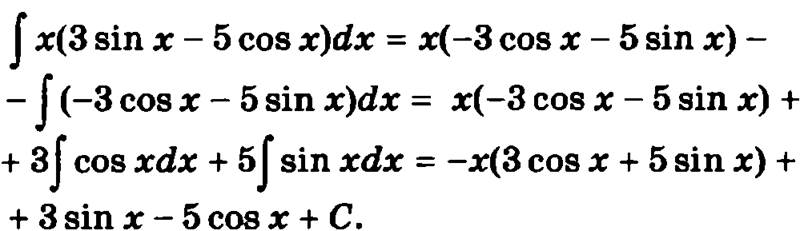
Метод замены переменной

Суть данного метода заключается в том, что вместо исходной переменной интегрирования, например, х, вводится новая переменная, например t, связанная со старой переменной соотношением t = ω(х) (ω(х) — дифференцируемая функция переменной х).

Пусть подынтегральная функция f(x) представима в виде f(x) = g(ω(x))(ω'(x).

Тогда исходный интеграл ∫ f(x)dx представим в виде

Переходя к новой переменной t = ω(x) и учитывая, что dt = ω’(x)dx, а функция g(t) имеет первообразную равную G(t), получим

Возвращаясь к первоначальной переменной интегрирования и подставляя вместо t функцию ω(x) окончательно получим

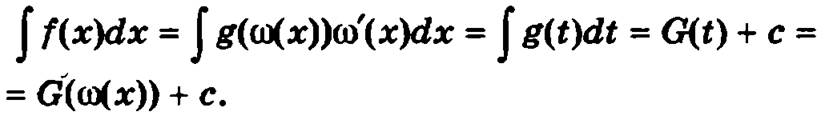
Пример.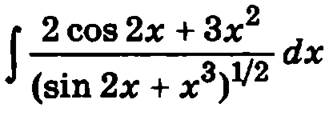

Обозначим через новую переменную интегрирований t выражение, стоящее в знаменателе подынтегральной функции t = sin 2х + х3, следовательно, dt = (2 cos 2х + 3x2)dx и исходный интеграл преобразуется к виду

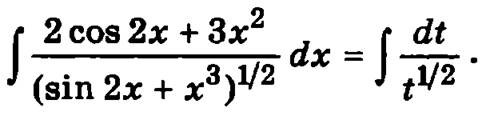
Вычислим полученный интеграл по переменной t и вернемся к старой переменной х, учитывая, что t = sin 2х + x3: