itle

В результате изучения параграфа 3 учащиеся должны уметь доказывать свойства 1°-3° прямоугольных треугольников; знать формулировки признаков равенства прямоугольных треугольников и уметь их доказывать; уметь применять свойства и признаки при решении задач типа № 254, 255, 256, 258, 260, 263, 265.

Урок 1. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

Цели: рассмотреть некоторые свойства прямоугольных треугольников и показать, как они применяются при решении задач.

Ход урока

I. Анализ результатов контрольной работы.

II. Изучение нового материала.

1. Устно решить задачу № 254 (использовать демонстрационный равнобедренный прямоугольный треугольник).

2. Решить задачу № 255 на доске и в тетрадях.

Дано: ΔСДЕ; СД = ДЕ; CF ⊥ ДЕ; ∠Д = 54°.

Найти: ∠ECF.

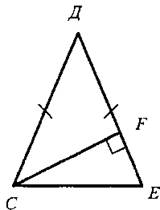
Решение:

По условию треугольник СДЕ - равнобедренный, тогда ∠Е = ∠ДСЕ = (180° - 54°) : 2 = 63° (углы при основании равнобедренного треугольника равны).

Так как CF ⊥ ДЕ по условию, то треугольник CFE - прямоугольный, в нем ∠CFE = 90°, ∠Е = 63°; тогда ∠ECF = 180° - (90° + 63°) = 27°.

Ответ: 27°.

3. Рассмотреть свойство 1° и посоветовать учащимся запомнить его, поскольку оно часто используется при решении задач.

4. Доказательство свойств 2° и 3° следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.

	Теорема	Обратная теорема
Дано	ΔABC; ∠A = 90° ∠B = 30°	ΔABC; ∠A = 90° АС = 1/2ВС
Доказать	АС = 1/2ВС	∠B = 30°

III. Закрепление изученного материала.

1. Устно решить задачи по готовым чертежам на доске:

1) Дано: ΔАВС (рис. 1).

Найти: углы ΔАВС.

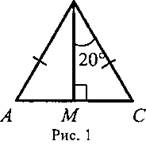
2) Дано: a || в (рис. 2).

Найти: углы треугольника MON.

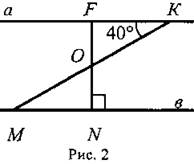
2. Решить задачу № 257 на доске и в тетрадях.

Дано: ΔАВС (рис. 3); ∠C = 90°, ∠ВАД = 120° - внешний угол; АС + АВ = 18 см.

Найти: АС и АВ.

Решение:

∠CAB = 180° - 120° = 60° (смежные углы), тогда ∠B = 90° - 60° = 30° (по свойству 1°); АС = 1/2AВ (свойство 2°; катет, лежащий против угла в 30°). По условию АС + АВ = 18 см; 1/2АВ + АВ = 18 см; 1 · 1/2AB = 18 см, АВ = 12 см; значит, АС = 18 - 12 = 6 (см).

Ответ: АВ = 12 см; АС = 6 см.

3. Решить задачу № 260.

Дано: ΔДМС (рис. 4); ДМ = МС; МО ⊥ ДС; ДМ = 15,2 см; МО = 7,6 см.

Найти: углы ΔДМС.

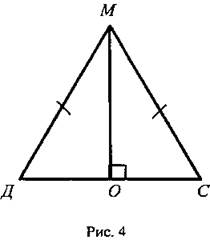
Решение:

Так как МО = 1/2ДМ, то по свойству 3° ∠Д = 30°, тогда ∠C = 30°, ∠M = 180° - (30° + 30°) = 180° - 60° = 120°.

Ответ: ∠Д = ∠C = 30°; ∠М = 120°.

IV. Итоги урока.

Домашнее задание: изучить п. 34; повторить пункты 15—33; ответить на вопросы 10 и 11 на с. 90; решить № 256, 259.