itle

Цели: закрепить навыки в решении задач на применение признаков равенства треугольников; проверить знания учащихся; подготовить учащихся к предстоящей контрольной работе.

Ход урока

I. Анализ самостоятельной работы.

II. Устный опрос учащихся по карточкам.

Вариант I

1. Сформулируйте первый признак равенства треугольников.

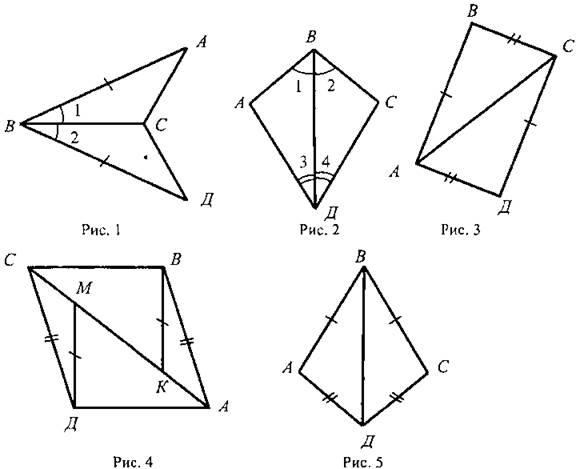
2. На рисунке 1 АВ = ДВ, ∠1 = ∠2. Докажите, что ΔABC = ΔДВС.

3. В треугольниках ABC и A1B1C1 АВ = А1В1; АС = А1С1 и ∠А = ∠А1. На сторонах АС и А1С1 отмечены точки Д и Д1 так, что СД = С1Д1. Докажите, что ΔАВД = ΔA1B1Д1.

Вариант II

1. Сформулируйте второй признак равенства треугольников.

2. На рисунке 2 ∠1 = ∠2, ∠3 = ∠4. Докажите, что ΔАВД = ΔСВД.

3. В треугольниках ABC и A1B1C1 проведены биссектрисы АД и А1Д1. Докажите, что ΔABC = ΔA1B1C1, если ДС = Д1С1, ∠C = ∠С1, ∠АДС = ∠А1Д1С1.

Вариант III

1. Сформулируйте третий признак равенства треугольников.

2. На рисунке 3 АВ = ДС, ВС = АД. Докажите, что ΔАВС = ΔСДА.

3. На рисунке 4 АВ = ДС, ВК = ДМ, AM = СК. Докажите, что ΔАДМ = ΔСВК.

Вариант IV

1. Сформулируйте свойство углов равнобедренного треугольника.

2. На рисунке 5 АВ = ВС, АД = ДС. Докажите, что ∠ВАД = ∠ВСД.

3. В равнобедренном треугольнике ABC на основании АС взяты точки Д и Е так, что АД = СЕ. Докажите, что треугольник ДВЕ равнобедренный.

Вариант V

1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.

2. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса ВД, ∠АВД = 37°, АС = 25 см. Найдите ∠В, ∠ВДС и ДС.

3. В равнобедренном треугольнике СДЕ с основанием ДЕ проведена биссектриса CF. Найдите CF, если периметр треугольника СДЕ равен 84 см, а треугольника CFE равен 56 см.

III. Решение задач.

1. Задача 1 (решение объясняет учитель на доске).

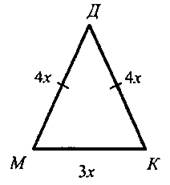
В равнобедренном треугольнике основание относится к боковой стороне как 3 : 4. Найдите стороны этого треугольника, если периметр его равен 33 см.

Дано : ΔМДК; МД = ДК; МК : МД = 3 : 4; Р = 33 см

Найти: МК, МД, ДК.

Решение:

Пусть на одну часть приходится х см, тогда МК = 3х см, МД = ДК = 4х см. По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3.

МК = 9 см, МД = ДК = 12 см.

Ответ: 9 см; 12 см; 12см.

2. Задача 2 (самостоятельно).

В равнобедренном треугольнике боковая сторона относится к основанию как 2 : 3. Найдите стороны треугольника, если периметр его равен 28 см.

3. Решить задачу № 175*.

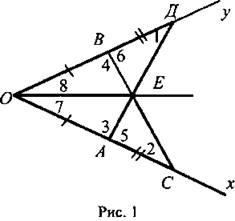
Запись решения задачи значительно упрощается, если ввести цифровые обозначения углов, как показано на рисунке 1.

Решение

1) ΔОАД = ΔОВС по двум сторонам и углу между ними, поэтому ∠1 = ∠2; ∠3 = ∠4.

2) Углы 3 и 5, а также 4 и 6 являются смежными, поэтому из равенства ∠3 = ∠4 следует, что ∠5 = ∠6.

3) ΔДВЕ = ΔСАЕ по стороне и двум прилежащим углам, поэтому BE = АЕ.

4) ΔОАЕ = ΔОВЕ по трем сторонам, значит, ∠7 = ∠8, то есть ОЕ - биссектриса угла ХОУ.

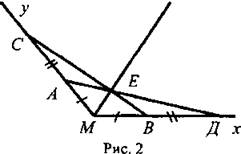
Для построения биссектрисы произвольного угла М на его сторонах откладываем отрезки МА = MB, АС = ВД, как показано на рисунке 2, и проводим отрезки АД и ВС. Затем проводим искомый луч ME, где Е - точка пересечения отрезков АД и ВС.

IV. Итоги урока.

Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15-23; решить задачи № 170, 171.