itle

Цели: изучить третий признак равенства треугольников и закрепить его знание в ходе решения задач; выработать у учащихся умение применять изученные теоремы при решении задач.

Ход урока

I. Проверка домашнего задания.

1. Обсудить решения домашних задач, ответить на вопросы учащихся.

2. Устный опрос учащихся с использованием вопросов 1-14 на с. 49-50.

3. Решение задач (устно) по готовым чертежам (см. рис. 1, 2) на применение первого и второго признаков равенства треугольников и свойств равнобедренного треугольника:

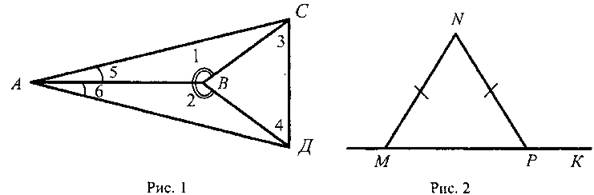
1) На рисунке 1 ∠1 = ∠2, ∠5 = ∠6, AC = 12 см, ВД = 5 cm, ∠4 = 21°. Найдите АД, ВC и ∠3.

2) На рисунке 2 MN = NP, ∠NPK = 152°. Найдите ∠NMP.

3) На рисунке 70, а учебника A1С = A1C1; CB1 = C1B1. Докажите, что ΔABC = ΔABC1.

II. Изучение нового материала.

1. Формулировка третьего признака равенства треугольников и его доказательство.

Можно дать формулировку третьего признака в таком виде: Два треугольника будут равными, если для каждой стороны одного треугольника найдется равная сторона в другом треугольнике.

Доказательство третьего признака равенства треугольников отличается от доказательств первого и второго признаков тем, что здесь не проводится наложение одного треугольника на другой. В процессе изучения теоремы о третьем признаке весьма полезна работа с рисунком 70, б и в учебника, по которому можно показать, что в случае, когда луч С1С совпадает с одной из сторон угла А1С1В1 или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С1С проходит внутри угла А1С1В1 или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С1С проходит внутри угла А1С1В1 (рис. 70, а). Можно также, после того как доказательство теоремы изложено учителем по рис. 70, а, предложить одному из учащихся доказать третий признак равенства треугольников для случая, изображенного на рисунке 70, в).

2. Треугольник - жесткая фигура (рис. 71 и 72).

III. Закрепление изученного материала.

1. Устно решить задачи по готовым чертежам (см. рис. 1-6).

Найдите пары равных треугольников и докажите их равенство (цель устной работы — учить учащихся читать чертеж по изображениям на нем равных элементов):

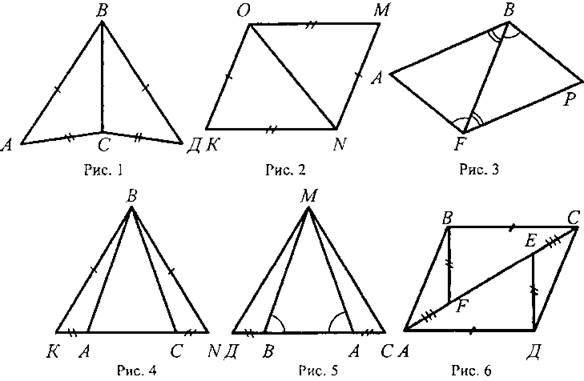
2. Устно решить задачу № 135.

3. Решить задачу № 138 (по рис. 75) на доске и в тетрадях:

Дано: АВ = СД и ВД = АС.

Доказать: а) ∠САД = ∠АДВ; б) ∠ВАС = ∠СДВ.

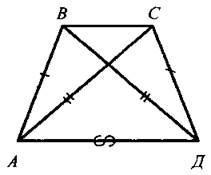
Доказательство:

1) Рассмотрим треугольник АВД и треугольник ДСА (можно отрезок ВС сначала стереть на доске, тогда учащиеся легко доказывают равенство этих треугольников):

АВ = СД (по условию); ВД = АС (по условию); АД - общая сторона (знак ∞) ⇒ ΔАВД - ΔДСА (третий признак по трем сторонам).

Отсюда имеем, что в равных треугольниках против равных сторон лежат равные углы, значит, ∠САД = ∠АДВ.

2) Рассмотрим треугольник ВАС и треугольник СДВ (восстанавливаем на доске отрезок ВС и стираем отрезок АД).

ВС - общая сторона этих треугольников. Аналогично доказывается равенство ΔВАС = ΔСДВ по третьему признаку. Тогда ∠ВАС = ∠СДВ.

IV. Итоги урока.

Домашнее задание: повторить пункты 15-19; изучить п. 20; решить задачи № 136, 137, 134.