Геометрия 7 класс поурочные планы
itle
Цели: повторить и закрепить изученный ранее материал; изучить второй признак равенства треугольников и выработать навыки использования первого и второго признаков равенства треугольников при решении задач; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Ответы на контрольные вопросы 4-13 на с. 50.
2. Решение задач по готовым чертежам с целью повторения первого признака равенства треугольников:
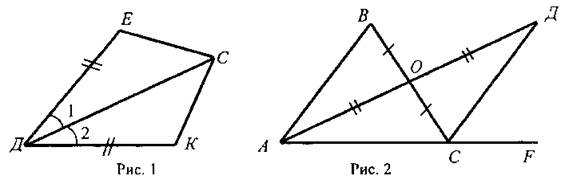
1) На рисунке 1 ДЕ = ДК, ∠1 = ∠2. Найдите ЕС, ∠ДCK и ∠ДKC, если КС = 1,8 дм; ∠ДCE = 45°, ∠ДEC = 115°.
2) На рисунке 2 ОВ = ОС, АО = ДО; ∠ACB = 42°, ∠ДCF = 68°.
Найдите ∠ABC.
II. Объяснение нового материала.
1. Выполнение учащимися практического задания: с помощью транспортира и масштабной линейки начертить треугольник ABC так, чтобы ∠А = 46°, ∠В = 58°, АВ = 4,8 см.
2. Формулировка и доказательство второго признака равенства треугольников (на доске и в тетрадях).
При доказательстве второго признака желательно отметить аналогию с доказательством первого признака: в том и другом случае равенство треугольников доказывается путем такого наложения одного треугольника на другой, при котором они полностью совмещаются.
III. Закрепление изученного материала.
1. Устно по готовым рисункам (рис. 3-7) решить задачи:
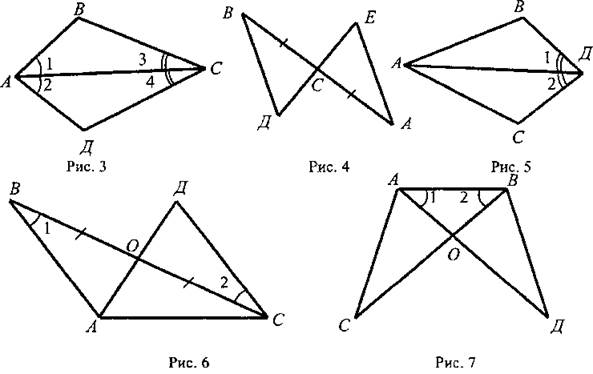
1) На рисунке 3 ∠1 = ∠2 и ∠3 = ∠4. Докажите, что ΔABC = ΔАДС.
2) На рисунке 4 АС = СВ, ∠A = ∠B. Докажите, что ΔВСД = ΔАСЕ.
3) На рисунке 5 луч АД - биссектриса угла ВАС, ∠1 = ∠2. Докажите, что ΔАВД = ΔАСД.
4) На рисунке 6 ВО = ОС, ∠1 = ∠2. Укажите равные треугольники на этом рисунке.
5) На рисунке 7 ∠1 = ∠2, ∠CAB = ∠ДВА. Укажите равные треугольники на этом рисунке.
2. Решить задачу № 121 (самостоятельно).
3. Решить задачу № 126 (по рис. 74).
4. Решить задачу № 127 (записать решение этой более сложной задачи на доске и в тетрадях):
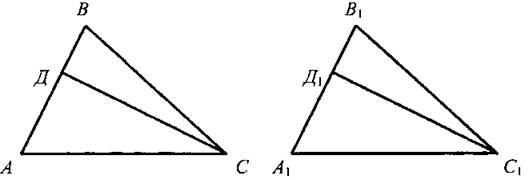
Дано: ΔАВС и ΔА1В1С1, АВ = A1B1; ВС = В1С1, ∠В = ∠В1; и Д ∈ АВ; Д1 ∈ A1B1; ∠АСД и ∠А1С1Д1.
Доказательство:
1) ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними, первый признак (АВ = A1B1; ВС = В1С1, ∠В = ∠В1 по условию), значит, ∠АСВ = ∠А1С1В1.
2) ∠ВСД = ∠АСВ - ∠АСД, ∠В1С1Д1 = ∠А1С1В1 - ∠А1С1Д1. Так как ∠АСВ = ∠А1С1В1 и ∠АСД = ∠А1С1Д1 (по условию), то ∠ВСД = ∠В1С1Д1.
3) ΔВСД = ΔВ1С1Д1 по стороне и прилежащим к ней углам, второй признак (ВС = В1С1, ∠В = ∠В1, ∠ВСД = ∠В1С1Д1), что и требовалось доказать.
IV. Итоги урока.
Домашнее задание: выучить доказательство теоремы из п. 19; решить задачи № 124, 125, 128.