Поурочные разработки по геометрии 10 класс
Зачет № 2 - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) способствовать усвоению учащимися перпендикулярности прямых и плоскостей;
2) теоремы о трех перпендикулярах в ходе решения задач;
3) развивать логическое мышление учащихся.
Ход урока
1. Организационный момент
2. Работа по карточкам
Карточка 1
1. Докажите теоремы, устанавливающие связь между параллельностью прямых и их перпендикулярностью к плоскости.
2. Решите задачу № 143 или № 213.
Карточка 2
1. Сформулируйте определение перпендикулярности прямой и плоскости. Докажите теорему, выражающую признак перпендикулярности прямой и плоскости.
2. Решите задачу № 131 или № 216.
Карточка 3
1. Докажите теорему о трех перпендикулярах.
2. Решите задачу № 150 или № 212.
Карточка 4
1. Сформулируйте определение угла между прямой и плоскостью. Расскажите о свойстве угла между прямой и плоскостью.
2. Решите задачу № 157 или № 206.
Карточка 5
1. Сформулируйте определение перпендикулярности двух плоскостей. Докажите теорему, выражающую признак перпендикулярности двух плоскостей.
2. Решите задачу № 171 или № 202.
Карточка 6
1. Докажите теорему о диагонали прямоугольного параллелепипеда.
2. Решите задачу № 195 или № 197.
Домашнее задание
Подготовиться к контрольной работе, просмотреть ранее решенные задачи.
Решение задач к зачету М 2 по теме «Перпендикулярность прямых и плоскостей»
Карточка № 1
Задача № 143
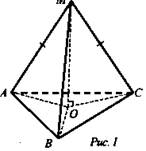
Дано: ΔАВС - правильный; АВ = 6 см; М ∉ (ABC); АМ = ВМ = СМ = 4 см (рис. 1).
Найти: расстояние от М до (ABC).
Решение:
1. Проведем МО ⊥ (ABC).
2. ΔАОМ = ΔВОМ = ΔСОМ (как прямоугольные по гипотенузе и катету) ⇒ АО = ВО = СО, то есть О - центр описанной около ΔАВС окружности.
3. ![]()
4. МО - расстояние от М до (ABC) и ΔМОС прямоугольный. ![]()
![]()
![]() (Ответ: 2 см.)
(Ответ: 2 см.)
Задача № 213
Дано: ΔАВС и DBC - прямоугольные; D проектируется в центр ΔАВС (рис. 2).
Вычислить угол между плоскостями ΔABC и ΔDBC.
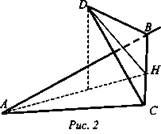
Решение: Пусть точка D1 проекция точки D на плоскость ABC. Тогда точка D1 является точкой пересечения медиан ΔАВС (центр ΔABC). АН - медиана, H - середина ВС, тогда ![]() откуда
откуда ![]() Причем АН ⊥ ВС и DH ⊥ ВС (по теореме о 3-х перпендикулярах), значит, ∠AHD - это угол между плоскостями треугольников. DH = АН (так как ΔАВС = ΔDBC), значит,
Причем АН ⊥ ВС и DH ⊥ ВС (по теореме о 3-х перпендикулярах), значит, ∠AHD - это угол между плоскостями треугольников. DH = АН (так как ΔАВС = ΔDBC), значит, ![]() Итак,
Итак, ![]() (Ответ:
(Ответ: ![]() )
)
Карточка № 2
2. Задача № 131
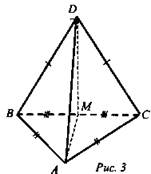
Дано: ABCD - тетраэдр, М - середина ВС, АВ = AC; DB = DC (рис. 3).
Доказать: ВС ⊥ (ADM).
Доказательство:
1. Так как АВ = АС, то ΔАВС равнобедренный. AM его медиана, следовательно, AM его высота, то есть АМ ⊥ ВС.
2. ΔBDC - равнобедренный, DM - медиана, а следовательно, высота. Таким образом, ВС ⊥ DM.
3. Получим ВС ⊥ AM, ВС ⊥ DM ⇒ ВС ⊥ (ADM). Что требовалось доказать.
Задача № 216
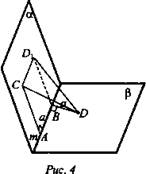
Дано: двугранный угол; m – ребро двугранного угла; ![]()
![]() (рис. 4).
(рис. 4).
Найти: CD.
Решение:
1. Проведем BD1 || АС так чтобы ABD1C был квадратом, то есть BD1 = а. Тогда ∠D1BD = 120°.
2. По условию BD ⊥ m, AC ⊥ m и AC || BD1, значит, BD1 ⊥ m, по теореме о трех перпендикулярах CD1 ⊥ DD1 и ∠CD1D = 90°. ΔCD1D - прямоугольный.
3. ΔD1BD: в нем D1B = BD = a; ∠D1BD = 120°. По теореме косинусов
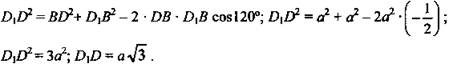
4. ![]() (Ответ: 2a.)
(Ответ: 2a.)
Карточка № .
Задача № 150
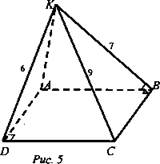
Дано: ABCD прямоугольник; АК ⊥ (ABC); KD = 6 см, KB = 7 см, КС = 9 см (рис. 5).
Найти: Р (К; (ABC)); Р (АК; CD).
Решение:
1. ![]()
2. АВ - проекция; КВ - наклонная ⇒ КВ ⊥ СВ.
3. ΔКВС: в нем КВ = 7 см; КС = 9 см; ∠B = 90°. По теореме Пифагора ![]()
![]()
4. ΔAKD: ![]()
![]()
5. ![]() (Ответ: AD = 4√2 см.)
(Ответ: AD = 4√2 см.)
Задача № 212
Дано: ΔАВС и ΔABD; точка С проекция точки D на (ABC); ∠((ABQ, (ABD)) = α, SΔABC = S (рис. 6).
Доказать: ![]()
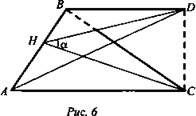
Доказательство: Проведем в ΔАВС высоту СН, тогда СН - проекция DH на плоскость (ABC) и по теореме о 3-х перпендикулярах DH ⊥ АВ, и значит, DH высота ΔABD, ∠DHC = α, но ΔDCH - прямоугольный, поэтому ![]()
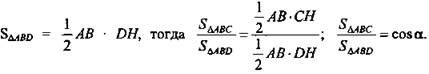 Отсюда
Отсюда ![]() что требовалось доказать.
что требовалось доказать.
Карточка № 4
Задача № 157
Дано: ABCD - ромб, AC ∩ BD = О, OK ⊥ (ABC), AC ⊥ BD (рис. 7).
Доказать: КМ = KN = КР = KL, то есть О - центр вписанной в ромб окружности.
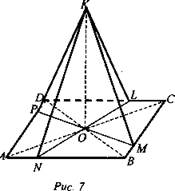
Доказательство:
1. OK ⊥ (ABC); KN ⊥ АВ; KN - наклонная. ON проекция ⇒ ON ⊥ AB.
2. Аналогично доказывается, что ОМ ⊥ ВС; ОР ⊥ AD; OL ⊥ DC.
3. ОМ = ON = OP = OL (как проекции равных наклонных).
4. К - равноудалена от всех сторон ABCD, следовательно, проектируется в центр О вписанной в него окружности.
5. ОК = 4,5 дм; АС = 6 дм; BD = 8 дм. Найти КМ. Так как AC ∩ BD = О середина АС и BD, то ВО = 4 дм; ОС = 3 дм. Тогда из ΔОВС:

(Ответ: 5,1 дм.)
Задача № 206
Дано: ΔABC; ∠A меньший; AM ⊥ (ABC); ВС = 8 см; АВ = 17 см; АС = 15 см (рис. 8).
Найти: Р (М; ВС) = МН.
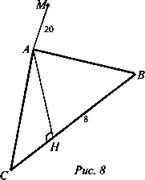
Решение: Так как против меньшего угла лежит меньшая сторона, то ВС = 8 см. Проведем высоту АН в ΔАВС. Тогда по теореме о 3-х перпендикулярах МН ⊥ ВС (так как АН ⊥ ВС), а следовательно, Р (М; ВС) = МН.
Пусть АВ = 17 см; АС = 15 см, ВН = х; СН = 8 - х по теореме Пифагора ![]() откуда
откуда ![]()
![]() Таким образом ВН = 8 см, это значит, ВН = ВС и АС ⊥ ВС, то есть АН = АС; АС = 15 см; АМ = 20 см. Так как ΔMAC прямоугольный, то
Таким образом ВН = 8 см, это значит, ВН = ВС и АС ⊥ ВС, то есть АН = АС; АС = 15 см; АМ = 20 см. Так как ΔMAC прямоугольный, то ![]()
![]() (Ответ: МН = 25 см.)
(Ответ: МН = 25 см.)
Карточка № .
Задача № 171
Дано: ![]()
![]() (рис. 9).
(рис. 9).
Найти: ∠(α; (ABC)).
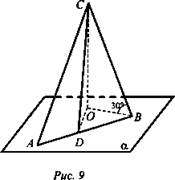
Решение:
1. Проведем СО ⊥ α, тогда ∠CBO = 30°. Пусть в ΔСОВ СО = а, тогда СВ = 2а.
2. Проведем CD ⊥ АВ, тогда АВ ⊥ DO и по теореме, обратной теореме о 3-х перпендикулярах, ∠CDO искомый.
3. Из ΔCDB известно, что ∠CBD = 45°, ![]()
4. Из ΔCDO: ![]() (Ответ: ∠(α; (ABC)) = 45°.)
(Ответ: ∠(α; (ABC)) = 45°.)
Задача № 202
Дано: ΔАВС, ∠C = 90°; CD - медиана; МА = MB = MC = 10 см. CD = 5 см (Рис. 10).
Найти: Р (М; (ABC))
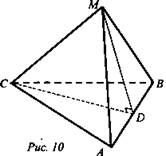
Решение:
1. Так как точка М равноудалена от всех вершин прямоугольного треугольника, то она проектируется в центр описанной около ΔАВС окружности, то есть в середину гипотенузы точка D.
2. MD ⊥ AD; CD - проекция наклонной СМ, значит, MD ⊥ CD и ΔCDM имеет ∠D = 90°.
3. СМ = 10 см; CD = 5 см, по теореме Пифагора ![]() (Ответ: 5√3 см.)
(Ответ: 5√3 см.)
Карточка № 6
Задача № 195
Дано: ABCDA1B1C1D1 прямоугольный параллелепипед, ![]()
![]() (рис. 11).
(рис. 11).
Найти: АВ; AD; АА1.
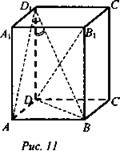
Решение:
1. BD1 = АС1 = 12 см.
2. АВ ⊥ (ADD1), значит, AD1 проекция BD1 на плоскость (AA1D1), значит, ∠AD1B = 30°.
3. Из ΔABD1 BD = 12 см; ∠A = 90°; ∠AD1B = 30°, значит, ![]()
4. ΔD1DB прямоугольный; ∠D = 90°; ∠BD1D = 45°, отсюда ∠D1BD = 45° и ![]()
5. Из ΔDAB: ![]() (Ответ: AB = AD = 6 cm; AA1 = 6√2 cm..
(Ответ: AB = AD = 6 cm; AA1 = 6√2 cm..
Задача № 197
Дано: ABCD - прямоугольник, BM ⊥ (ABC) (рис. 12).
Доказать: CD ⊥ (МВС).
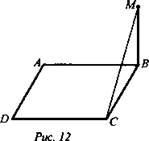
Доказательство: Так как MB ⊥ (ABC), то BМ ⊥ CD, и так как ABCD прямоугольник, то CD ⊥ ВС.
По признаку перпендикулярности прямой и плоскости CD ⊥ (МВС), что требовалось доказать.