Контрольная работа по теме «Перпендикулярность прямых и плоскости» - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цель урока:

- проверить знания учащихся по данной теме, выявить проблемы в знаниях.

Ход урока

Контрольная работа проводится по вариантам (по карточкам).

I уровень

Вариант I

1. Длина стороны ромба ABCD равна 5 см, длина диагонали BD равна 6 см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 8 см.

Дано: ABCD - ромб. АВ = 5 см. BD = 6 см. OK ⊥ (ABC), OK = 8 см (рис. 1).

Найти: КА, КВ, КС, KD.

Решение: - свойство диагоналей ромба. KB1, KC1, KA1, KD - наклонные к плоскости (ABCD) из одной точки. КА = КС, КВ = KD.

1) Из ΔКОВ: ∠O = 90°; КО = 8 см, ВО = OD = 3 см. По теореме Пифагора

2) Из ΔВОА: ∠O = 90°; ОВ = 3 см, АВ = 5 см. По теореме Пифагора Из ΔКОА: ∠O = 90°. По теореме Пифагора (Ответ: )

2. Длина катета прямоугольного равнобедренного треугольника равна 4 см. Плоскость α, проходящая через катет, образует с плоскостью треугольника угол, величина которого равна 30°. Найдите длину проекции гипотенузы на плоскость α.

Дано: (рис. 2).

Найти: КВ.

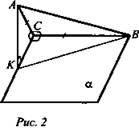
Решение: КСВА - двугранный угол. СВ - ребро двугранного угла. AC ⊥ СВ, КС ⊥ СВ, ∠ACK - линейный угол двугранного угла. По условию АВ - наклонная к плоскости α из точки А. КВ - проекция наклонной. Из ΔКАС: (по условию), (как катет, лежащий против угла в 30°). КС2 = АС2 - АК2 - по теореме Пифагора. КС2 = 42 - 22 = 12. Из ΔКСВ: По теореме Пифагора (Ответ: КВ = 2√7 см.)

Вариант I.

№ 1

Длины сторон прямоугольника равны 8 и 6 см. Через точку О пересечения его диагоналей проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин прямоугольника, если ОК = 12 см.

Дано: ABCD - прямоугольник; АВ = DC = 6 см; AD = ВС = 8 см. AC ∩ BD = 0; OK ⊥ ABCD; ОК = 12 см (рис. 3).

Найти: КА, КВ, КС, KD.

Решение: Из точки К к плоскости проведены наклонные КА1, КВ, КС, KD. Так как КО ⊥ (ABC), то ОА, ОВ, ОС, OD - проекции наклонных. АС = ВС. КО ⊥ (ABC) - диагонали прямоугольника ⇒ АО = ОС = ОВ = OD. Из ΔBAD: ∠A = 90°, АВ = 6 см, AD = 8 см. По теореме Пифагора Из ΔКОВ:

(Ответ: КА = КВ = КС = КР = 13 см.)

Вариант I.

№ 2

Длины сторон треугольника ABC соответственно равны: ВС = 15 см, АВ = 13 см, АС = 4 см. Через сторону АС проведена плоскость а, составляющая с плоскостью данного треугольника угол 30°. Найдите расстояние от вершины В до плоскости α.

Дано: ΔАВС. ВС = 15 см, АВ = 13 см, АС = 4 cm. АС ⊂ α. ∠BACK = 30°. BK ⊥ α (рис. 4).

Найти: ВК.

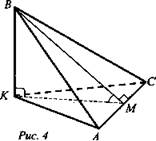
Решение: BACK - двугранный угол. АС - ребро двугранного угла. ∠BMK - линейный угол двугранного угла. ∠BMK = 30°.

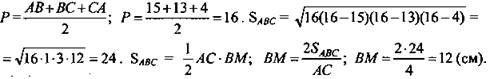
Из ΔВКМ: ∠K = 90°; ∠M = 30°. Катет, лежащий против угла 30°, равен 1/2 гипотенузы, то есть ВК = 1/2ВМ = 6. (Ответ: 6 см.)

II уровен.

Вариант I

1. Диагональ куба равна 6 см.

Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней.

Дано: ABCDA1B1C1D1 — куб. DB = 6 см (рис. 5).

Найти: a) DC- ? б) cos ∠CB1D - ?

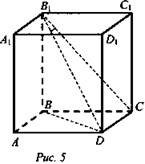
Решение:

а) Мы знаем теорему d2 = а2 + b2 + с2. Так как куб - частный случай параллелепипеда, его ребра равны, то d2 = 3а2, где а - ребро куба. 62 = 3а2; а2 = 12; а = 2√3 . Итак, DC = 2√3 см.

б) Углом между DB1 и плоскостью (ВВ1С1), является ∠DB1C, так как DC ⊥ (ВВ1С1), и В1С - проекция DB1 на плоскость (BB1C1). В ΔDCB1: В1С - диагональ квадрата ВВ1С1С со стороной 2√3 см ⇒ (Ответ: )

2. Сторона АВ ромба ABCD равна а, один из углов ромба равен 60°. Через сторону АВ проведена плоскость α на расстоянии a/2 от точки D.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла DABM, M ∈ α.

в) Найдите синус угла между плоскостью ромба и плоскостью α.

Дано: ABCD - ромб; (рис. 6).

Найти: а) расстояние от С до α; б) линейный угол двугранного угла DABM; в) sin ∠PKD.

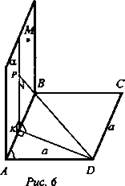
Решение:

а) Это значит, все точки данной прямой удалены одинаково от плоскости α, то есть если расстояние от D равно a/2, то и расстояние от С тоже равно a/2.

б) По определению, двугранные углы измеряются линейными углами. Все линейные углы одного двугранного угла равны. Поэтому достаточно построить любой угол двугранного угла DABM. DK ⊥ АВ, DK ⊂ (ABC), АВ - ребро двугранного угла. В плоскости α КР ⊥ АВ. ∠PKD - линейный угол данного двугранного угла.

в) Из ΔKPD: Из ∠AKD: (по теореме Пифагора из ΔAKD); (Ответ: )

Вариант II

1. Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 2√6 см, а его измерения относятся как 1:1:2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания.

Дано: АС1 - прямоугольный параллелепипед. ABCD - квадрат, B1D = 2√6 см; AD : DC : DD1 = 1 : 1 : 2. (рис. 7).

Найти: a) AD, DC, DD1; б) sin ∠BDB1.

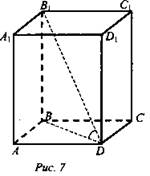
Решение:

а) По теореме о свойстве диагонали параллелепипеда имеем: Пусть AD = х см, тогда

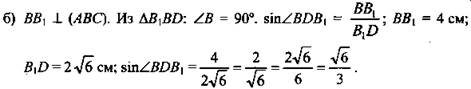
(Ответ: )

2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость а на расстоянии a/2 от точки В.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла BADM, M ∈ α.

в) Найдите синус угла между плоскостью квадрата и плоскостью α.

Дано: ABCD - квадрат. (рис. 8).

Найти: а) расстояние от С до α; б) показать линейный угол двугранного угла BADM; в) sin ∠BAK.

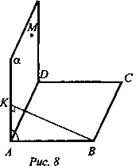
Решение:

а) Так как точки В к С лежат на одной прямой ВС || AD, a AD ⊂ α, то ВС || α и расстояние от точки В и С до плоскости α одинаковое, то есть a/2.

б) Любой двугранный угол измеряется линейным углом. Все они равные по величине для данного двугранного угла. Поэтому достаточно построить один угол в любом месте. AD - ребро двугранного угла. АВ ⊥ AD, АВ ⊂ (ABC). В плоскости а из точки А проводим перпендикуляр к AD. АК ⊥ AD. ∠KAB - линейный угол двугранного угла BADM.

в) Из ΔАКВ: ∠K = 90°; АВ = а; КВ = a/2; так как катет равен половине гипотенузы, то угол КАВ = 30°, то есть (Ответ: а) a/2; в) 1/2.)