Вариант № 23 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Магазин, делая наценку 50%, продаёт канцелярские наборы по цене 90 рублей за штуку. Какое наибольшее число таких наборов может закупить хозяиц этого магазина на 4300 рублей?

В2. На рисунке 134 точками показана цена акций компании «Сургутнефтегаз» на момент закрытия биржевых торгов во все рабочие дни января 2011 года. По горизонтали указываются числа месяца, по вертикали — цена акции в рублях. Для наглядности точки на рисунке соединены линией. Определите по рисунку, сколько дней рассматриваемого периода цена акции «Сургутнефтегаза» на момент закрытия торгов была выше 34 рублей за акцию.

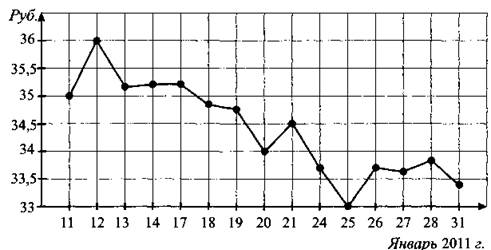
Рис. 134.

В3. Точки О(0; 0), А(2; 5), В(8; 7), С(6; 2) являются вершинами четырёхугольника (см. рис. 135). Найдите ординату точки пересечения его диагоналей Р.

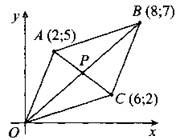
Рис. 135.

В4. Клиент хочет арендовать автомобиль на сутки для поездки протяжённостью 700 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды. Помимо аренды, клиент обязан оплатить стоимость топлива для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешёвый вариант?

Автомобиль	Топливо	Расход топлива (л на 100 км)	Арендная плата (руб. за 1 сутки)
1	Дизельное	8	2800
2	Бензин	11	2500
3	Газ	15	2600

Цена дизельного топлива — 20 рублей за литр, бензина — 25 рублей за литр, газа — 17 рублей за литр.

В5. Найдите корень уравнения log₂₅ (5 + х) = log₅(2х). Если уравнение имеет более одного корня, то укажите меньший из них.

В6. Основания равнобедренной трапеции равны 8√7 и 12√7, а боковая сторона равна 8. Найдите синус острого угла трапеции.

В7. Найдите значение выражения при b ∈ (3; 13).

В8. На рисунке 136 изображён график некоторой функции у = f(x). Функция — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

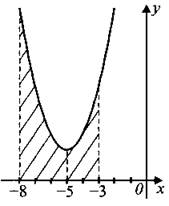
Рис. 136.

В9. Конус описан около правильной четырёхугольной пирамиды со стороной основания 6 и высотой 9/π. Найдите его объём.

В10. Пете нужно забить в стенку гвоздь. Если гвоздь стальной, то он согнётся с вероятностью 0,2, а если гвоздь железный, то он согнётся с вероятностью 0,6. На столе лежат 14 стальных и 6 железных гвоздей. Петя берёт первый попавшийся гвоздь со стола и пытается забить его в стенку. Найдите вероятность того, что этот гвоздь согнётся.

В11. Объём куба равен 20. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины (см. рис. 137).

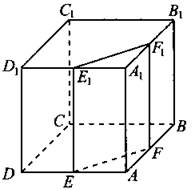
Рис. 137.

В12. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t², где h — расстояние в метрах, t — время падения в секундах. До начала дождя время падения камешков составляло 1,2 с. На сколько метров должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,4 с?

В13. Ксюша решила прочесть книгу объёмом 672 страницы. Ежедневно она читает на одно и то же количество страниц больше по сравнению с предыдущим днём. Известно, что в первый день она прочла 12 страниц. Определите, сколько страниц она прочла в последний день, если всего на чтение этой книги девочка потратила 16 дней.

В14. Найдите наименьшее значение функции

Часть 2

С1. Решите уравнение х⁴ — 10х³ + 35х² — 50х + 25 = 0.

С2. В правильной треугольной призме с площадью основания S₀ = 3 проведено сечение через сторону нижнего основания и противоположную вершину верхнего основания. Площадь этого сечения S_c = 5. Найдите угол, который сечение образует с плоскостью основания.

С3. Решите неравенство 30 arcsin² х + 23π arcos x — 8,5π² ≥ 0.

С4. Определите, какое наименьшее значение может принимать площадь треугольника, одна из сторон которого a = 3, а радиус вписанной окружности r = 1.

С5. Определите, при каких значениях параметра а число а лежит между корнями уравнения а²х² + (35а — 10а²)x — 50а + 24 = 0.

С6. Дана сумма n слагаемых:

Найдите:

а) сумму четырёх слагаемых 54;

б) все натуральные значения п, при которых S_n ≥ 1/4.

в) все натуральные значения п, при которых S_n ≤ 1/5.

г) все натуральные значения п, при которых