Вариант № 22 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Магазин покупает чайники по оптовой цене 420 рублей за штуку, а продаёт с наценкой 25%. Какое наибольшее число таких чайников можно купить в этом магазине за 3400 рублей?

В2. На рисунке 130 точками показано суточное количество осадков, выпадавших с 16 по 28 марта. По горизонтали указываются числа месяца, по вертикали — количество осадков в миллиметрах, выпавшее в соответствующий день. Для наглядности точки на рисунке соединены линией. Определите по рисунку количество дней рассматриваемого периода, когда выпадало 4 и более миллиметров осадков.

В3. Площадь круга равна 9/π. Найдите длину окружности, ограничивающей данный круг.

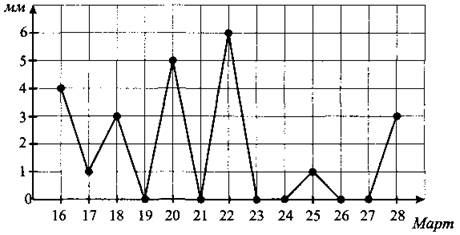
Рис. 130.

В4. Из пункта Л в пункт D ведут три дороги (см. рис. 131, расстояние между пунктами указано в километрах). Через пункт В едет грузовик со средней скоростью 28 км/ч, через пункт С едет легковой автомобиль со скоростью 58 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется автобус со средней скоростью 44 км/ч. Все три машины одновременно выехали одновременно из пункта А. Какой автотранспорт добрался до D раньше других? В ответе укажите, сколько минут он находился в дороге.

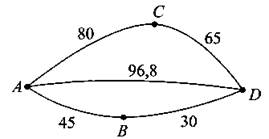
Рис. 131.

В5. Решите уравнение 2^{8 - 2х} = 2^х2. Если оно имеет несколько корней, то в ответе укажите меньший из них.

В6. Основания равнобедренной трапеции равны 8 и 16. Косинус острого угла трапеции равен 0,8. Найдите высоту трапеции.

В7. Найдите значение выражения

В8. На рисунке 132 изображён график функции у = f(x) и отмечены точки —5, —4, —2, —1, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

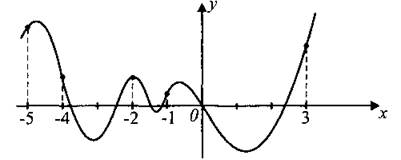
Рис. 132.

В9. В кубе ABCDA₁B₁C₁D₁ точка М — середина ребра АА₁, точка F — середина ребра A₁B₁, точка N — середина ребра A₁D₁. Найдите угол NFM. Ответ дайте в градусах.

В10. Две фабрики выпускают одинаковые лампочки. Первая фабрика выпускает 60% этих лампочек, вторая — 40%. Среди продукции первой фабрики 3%'лампочек дефектные, среди продукции второй фабрики — 2%. Найдите вероятность того, что случайно купленная в магазине лампочка окажется дефектной.

В11. Во сколько раз уменьшится объём конуса (см. рис. 133), если диаметр его основания уменьшить в 2,5 раза, а высоту оставить прежней?

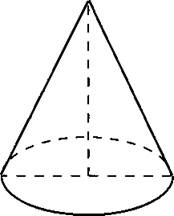
Рис. 133.

В12. Перед отправкой тепловоз издал гудок с частотой f₀ = 490 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону 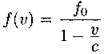(Гц), где с — скорость звука в воздухе (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а с = 340 м/с. Ответ выразите в м/с.

В13. Поезд, двигаясь со скоростью 70 км/ч, проезжает мимо платформы за 45 секунд. Определите длину платформы (в метрах), если длина поезда 600 м.

В14. Найдите точку минимума функции

Часть 2

С1. а) Решите уравнение cos x(tg х — cos х) = —sin² х.

б) Найдите все корни этого уравнения, принадлежащие промежутку [4π; 13π/2].

С2. В основании прямой призмы лежит треугольник со сторонами 5, 12, 13. Некоторая плоскость отсекает от боковых рёбер этой призмы, проходящих через вершины большего и среднего углов основания, отрезки, равные 10 каждый (считая от плоскости основания), а от ребра, проходящего через вершину меньшего угла основания, — отрезок 15 соответственно. Найдите объём и площадь полной поверхности фигуры, ограниченной плоскостью основания призмы, плоскостями боковых граней и плоскостью сечения.

С3. Решите систему неравенств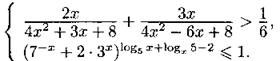

С4. В трапеции с боковыми сторонами 13 и 20 и основаниями б и 27 проведена диагональ. В каждый из образовавшихся треугольников вписана окружность. Найдите расстояние между точками касания вписанных окружностей с проведённой диагональю.

С5. При каких значениях а уравнение имеет единственное решение?

С6. Имеется шестьдесят двухлитровых сосудов, содержащих 1 см³, 2 см³, 3 см³, ..., 60 см³ воды. Из сосуда А разрешается перелить в сосуд Б столько воды, сколько имеется в В (при условии, что в A не меньше воды, чем в В). Можно ли после нескольких переливаний:

а) добиться того, чтобы в сосудах вновь оказалось 1 см³, 2 см³, 3 см³, ..., 60 см³ воды, но при этом ни в одном из них не было бы первоначального её количества?

б) добиться того, чтобы в каких-то девяти сосудах оказалось по 5 см³ воды, а в остальных — 10 см³,11 см³,12 см³, ..., 60 см³ воды?

в) перелить всю воду в один сосуд?