Математика сборник задач для подготовки к ЕГЭ
Вариант № 20 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Часть 1
В1. Тетрадь стоит 16 рублей. Сколько рублей заплатит покупатель за 40 тетрадей, если при покупке более 30 тетрадей магазин делает скидку 15% от стоимости всей покупки?
В2. На графике (см. рис. 117) показано изменение скорости движения автомобиля в зависимости от времени. На оси абсцисс отмечается время движения в часах, на оси ординат — скорость в километрах в час. Сколько часов автомобиль двигался со скоростью не менее 70 км/ч?
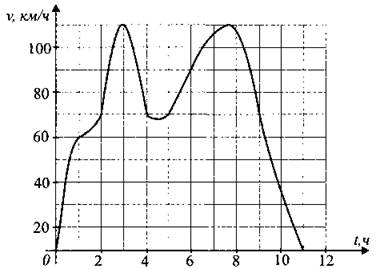
Рис. 117.
В3. Найдите площадь четырёхугольника, изображённого на рисунке 118.
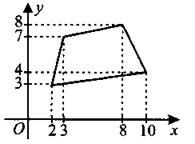
Рис. 118.
В4. Строительной фирме нужно приобрести 90 кубометров строительного бруса у одного из трёх поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
|
Поставщик |
Цена бруса (руб. за 1 м3) |
Стоимость доставки |
Дополнительные условия |
|
А |
4500 |
20000 |
При заказе на сумму свыше 500 тыс. руб. доставка бесплатно |
|
Б |
4700 |
14000 |
При заказе на сумму свыше 200 тыс. руб. доставка бесплатно |
|
В |
4600 |
10000 |
При заказе на сумму свыше 450 тыс. руб. доставка бесплатно |
В5. Найдите корень уравнения ![]() Если уравнение имеет более одного корня, то в ответе укажите больший из них.
Если уравнение имеет более одного корня, то в ответе укажите больший из них.
В6. Два угла вписанного в окружность четырёхугольника равны 120° и 82° (см. рис. 119). Найдите меньший из оставшихся углов. Ответ дайте в градусах.
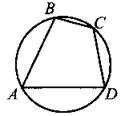
Рис. 119.
В7. Найдите значение выражения ![]()
B8. На рисунке 120 изображён график некоторой функции у = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(9) — F(-2), где F(x) — одна из первообразных функции f(x).
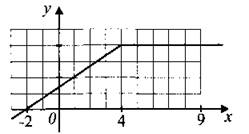
Рис. 120.
В9. Найдите угол ABD многогранника, изображённого на рисунке 121. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
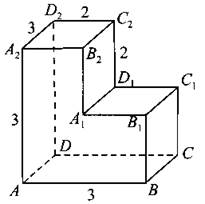
Рис. 121.
В10. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая команда начнёт игру с мячом. Команда «Вымпел» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Вымпел» выиграет жребий ровно один раз.
В11. Найдите объём V части конуса, изображённой на рисунке 122. В ответе укажите V/π.
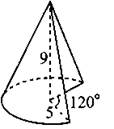
Рис. 122.
В12. Находящийся в воде водолазный колокол, содержащий v = 40 молей воздуха при давлении p1 = 1,3 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением ![]() (Дж), где α = 3,5 — постоянная, Т = 300 К — температура воздуха, р1 (атм) — начальное давление, а р2 (атм) — конечное давление воздуха в колоколе. До какого наибольшего давления р2 можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 126 000 Дж? Ответ приведите в атмосферах.
(Дж), где α = 3,5 — постоянная, Т = 300 К — температура воздуха, р1 (атм) — начальное давление, а р2 (атм) — конечное давление воздуха в колоколе. До какого наибольшего давления р2 можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 126 000 Дж? Ответ приведите в атмосферах.
В13. Вторая труба пропускает в минуту на 6 л воды меньше, чем первая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 140 л она заполнит на 5 минут быстрее, чем вторая труба заполняет резервуар объёмом 100 л?
В14. Найдите наибольшее значение функции у = 4 sin x + 4х — 2π на отрезке [0; π/2].
Часть 2
С1. а) Решите уравнение 1 + sin 2х — sin х — cos х = 0.
б) Укажите корни, принадлежащие промежутку (-3π/2; 0].
С2. Дан куб ABCDA1B1C1D1. Точки М и N — середины рёбер ВВ1 и DD1 соответственно. Найдите угол между плоскостями AMN и CMN.
С3. Решите систему неравенств ![]()
С4. В квадрате, длина стороны которого равна 1, расположен прямоугольник площадью 1/2 так, что на каждой стороне квадрата лежит ровно одна вершина прямоугольника. Найдите длину диагонали прямоугольника.
С5. При каких положительных значениях параметра а неравенство ![]() справедливо при всех х > 6?
справедливо при всех х > 6?
С6. Среди 100 отдыхающих провели опрос, в результате которого выяснилось, что 95 из них были в Сочи, 85 — в Анапе, 75 — в Туапсе и 65 — в Геленджике.
а) Какое наибольшее количество отдыхающих могло быть во всех курортных городах?
б) Какое наименьшее количество отдыхающих могло быть во всех курортных городах?