Вариант № 19 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. На счету Машиного мобильного телефона было 67 рублей, а после разговора с Леной осталось 10 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 1 рубль 50 копеек?

В2. На графике (рис. 112) показано изменение скорости движения автомобиля в зависимости от времени. На оси абсцисс отмечается время движения в часах, на оси ординат — скорость в километрах в час. Сколько часов автомобиль двигался со скоростью не более 70 км/ч?

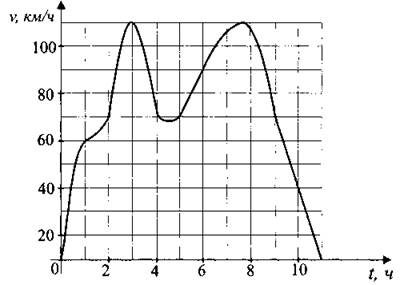
Рис. 112.

В3. Найдите площадь четырёхугольника, вершины которого имеют координаты (0; 1), (1; 7), (7; 6), (6; 0) (см. рис. 113).

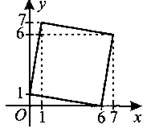
Рис. 113.

В4. Строительной фирме нужно приобрести 80 кубометров пенобетона у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей стоит самая дешёвая покупка с доставкой?

Поставщик	Стоимость пенобетона (руб. за 1 м3)	Стоимость доставки	Дополнительные условия
А	2700	6800
Б	3100	3200	При заказе на сумму свыше 250 000 руб. доставка бесплатно
В	2800	13500	При заказе на сумму свыше 200 000 руб. доставка бесплатно

В5. Найдите корень уравнения log₃ (37x + 7) = 4.

В6. PQ и KF — диаметры окружности с центром в точке О (см. рис. 114). Угол PQF равен 42°. Найдите угол КОР. Ответ дайте в градусах.

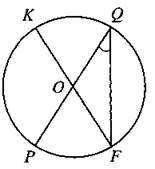
Рис. 114.

В7. Найдите значение выражения при b = 29.

В8. На рисунке 115 изображён график некоторой функции у = f(x). Функция F(x) = —x³ — 9х² — 15х + 18 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

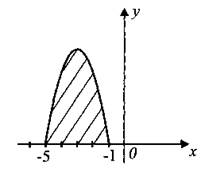
Рис. 115.

В9. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер АВ = 3√7, AD = 9, АА₁ = 6. Найдите синус угла между прямыми CD и A₁C₁.

В10. Одновременно бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.

B11. Рёбра тетраэдра равны 3. Найдите площадь сечения, проходящего через середины четырёх его рёбер (см. рис. 116).

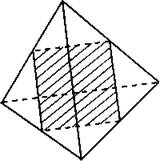
Рис. 116.

В12. Ёмкость высоковольтного конденсатора в телевизоре С = 3 ∙ 10^-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 10⁷ Ом. Во время работы телевизора напряжение на конденсаторе U₀ = 32 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением где α = 0,7 — постоянная. Определите наибольшее возможное напряжение на конденсаторе (в киловольтах), если после выключения телевизора прошло не менее 42 с.

В13. Велосипедист проехал расстояние в 120 км от А до В с постоянной скоростью. На следующий день он проехал это же расстояние от В до А со скоростью на 5 км больше прежней. По дороге он сделал две остановки по 1 часу, однако в пункт А он добрался за то же время, что и потратил на дорогу из А в В. Найдите скорость велосипедиста на пути из Б в А. Ответ дайте в км/ч.

В14. Найдите точку минимума функции у = (х² + 7х + 7)е^{х - 5}.

Часть 2

С1. а) Решите уравнение

б) Укажите корни, принадлежащие промежутку [—3π; —π).

С2. В кубе ABCDA₁B₁C₁D₁ найдите угол между плоскостями A₁C₁D и BC₁D.

С3. Решите систему неравенств

С4. В квадрате, длина стороны которого равна 8, расположен прямоугольник так, что на каждой стороне квадрата лежит ровно одна вершина прямоугольника. Найдите площадь прямоугольника, если известно, что длина его диагонали равна 4√5.

С5. При каких положительных значениях параметра а неравенство справедливо при всех х > 9?

С6. В порту 90% населения говорит по-английски, 85% — по-немецки, 80% — по-французски и 75% — по-испански.

а) Какой наибольший процент населения может говорить на всех четырёх языках сразу?

б) Какой наименьший процент населения может говорить на всех четырёх языках сразу?