Урок 1 - РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ

Цели: повторить алгоритмы построения параболы, правила решения квадратных уравнений; объяснить правило решения квадратных неравенств; формировать умение решать различные неравенства.

Ход урока

I. Организационный момент.

II. Анализ самостоятельной работы.

Если с самостоятельной работой не справилось большинство учащихся, то необходимо провести работу по решению линейных неравенств.

6x > 72; 3x < –12; –7x ≥ 49; –11x < –33;

4x – 6 > 6x + 14; 13 – 5x ≤ x – 5; 7x + 1 < 21 – 3x; 5 – 8x < 21 – 5x;

5 – 2x ≤ 1 – (x – 2); 3 – x ≤ 1 – 7(x + 1); 6 – 6(x – 3) ≥ 2(x + 1) – 10; x – 5(x – 4) > 6x + 20.

III. Актуализация знаний.

Учащиеся должны вспомнить правила построения параболы и правила решения квадратных уравнений. Для этого на доске разбирается построение графиков следующих функций:

а) y = x2 – 4x + 3;

б) y = –x2 + 2x + 3.

Находятся точки пересечения данных графиков с осью абсцисс.

IV. Объяснение нового материала.

Учитель выводит понятие квадратного неравенства, алгоритм решения квадратного неравенства.

Для лучшего закрепления материала можно приготовить плакат с алгоритмом решения квадратного неравенства.

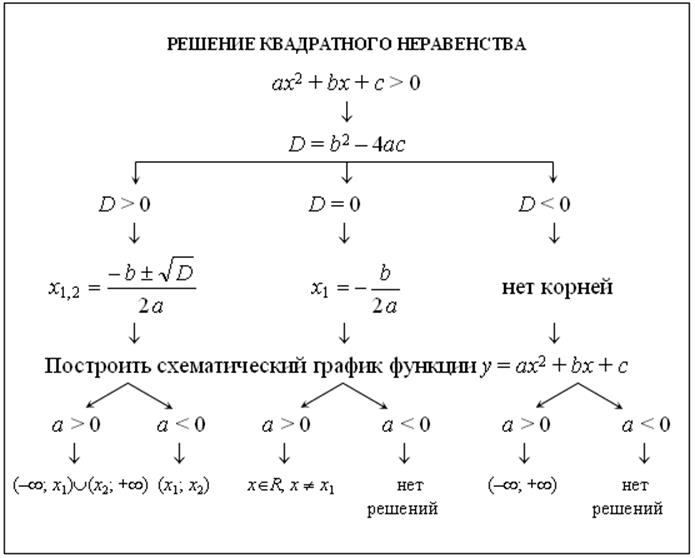
Рассмотреть решение неравенства по данному алгоритму:

x2 + 6x – 16 > 0

1) Найдем дискриминант трехчлена

x2 + 6x – 16

D = b2 – 4ac,

D = 36 – 4 ⋅ (–16) = 100 > 0

Следовательно, имеется два действительных корня трехчлена.

2) Найдем корни этого трехчлена, решив уравнение.

x2 + 6x – 16 = 0

x1 = –8, x2 = 2.

3) Построим схематический график функции y = x2 + 6x + 16.

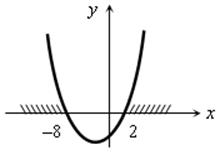
4) О т в е т: x (–∞; –8)(2; +∞).

V. Закрепление нового материала.

1) Рассмотреть решение неравенств № 34.1; 34.2; 34.3; 34.8.

2) Рассмотреть решения неравенств № 34.11; 34.12.

3) Сильным учащимся можно предложить задания типа:

Для каждого a решите неравенство:

а) (x – 3)2 < a; б) (3 – 4x) 2 ≤ a – 1; в) |x – a|(x – 3) < 0;

г) (x – a)2(x – 7) ≥ 0; д) (x – a)|x – 5| ≤ 0.

Р е ш е н и е:

б) (3 – 4x)2 ≤ a – 1;

9 – 24x + 16x2 ≤ a – 1;

16x2 – 24x + 10 – a ≤ 0;

16x2 – 24x + 10 – a = 0;

a = 16, b = –24, c = 10 – a;

D = b2 – 4ac = 576 – 640 + 64a = 64(a – 1);

1. При a = 1 D = 0;

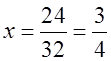– единственное решение при условии a = 1.

2. При a < 1 D < 0.

При заданном значении a < 1 неравенство не имеет решения.

3. При a > 1 D > 0;

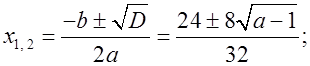
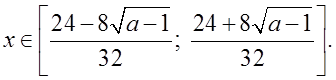
VI. Подведение итогов.

Домашнее задание: прочитать материал параграфа 34, выучить алгоритм решения квадратных неравенств. Решить задачи № 34.5; 34.6; 34.10.