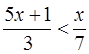Поурочные разработки по Алгебре 8 класс
Урок 3 - РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ
Цели: рассмотреть решения неравенств различной сложности, а также решение задач, с помощью неравенств; развивать умение решать линейные неравенства.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
К доске вызываются ученики выполнить задания с карточек:
Карточка 1 5x – 3 > 3x + 17 |
Карточка 2 3(3x – 1) < 2(5x – 7) |
Карточка 3 2(1 – x) ≥ 5x – (3x + 2) |
Карточка 4
|
III. Актуализация знаний.
Пока выполняются задания с карточек, остальные учащиеся по вариантам решают самостоятельно № 33.20.
По прошествии некоторого времени проверяются задания на доске, с полным объяснением, задания в тетрадях, а так же номера домашней работы.
IV. Решение задач.
1) Разобрать решение заданий № 33.28 (а, б); 33.29; 33.31; 33.35; 33.38.
2) Рассмотреть решение дробных неравенств:
а) 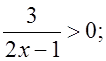 б)
б) 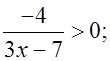 в)
в) 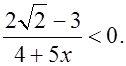
Решение данных неравенств происходит по алгоритму:
1) определить знак числителя;
2) по знаку неравенства и знаку числителя составить неравенство для знаменателя;
3) решить получившееся неравенство.
3) Сильным ученикам предложить рассмотреть решение сложного неравенства:
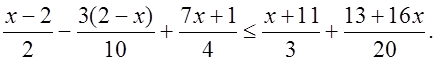
Р е ш е н и е:
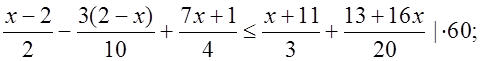
![]()
![]()
![]()
85x ≤ 340;
x ≤ 4.
О т в е т: (–∞; 4].
V. Самостоятельная работа.
Вариант 1 |
Вариант 2 |
|
1) Какие из чисел –3, 0, 4, 11 являются решениями неравенства: |
||
5x – 7 > 3 |
10 – 2x > 8 |
|
2) Решите неравенства: |
||
а) 7x < 49; б) 4x – 7 > 13 – x; в) 25 – x > 2 – 3(x – 6); г) 2(x – 1) ≤ 5x – 4(2x +1). |
а) 6x > 42; б) 5 – 5x > 11 – 7x; в) 5(x + 4) < 2(4x – 5); г) 4(x – 1) – (9x – 5) ≥ 6. |
|
О т в е т ы:
Задание |
1 |
2 (а) |
2 (б) |
2 (в) |
2 (г) |
I |
4, 11 |
x < 7 |
x > 4 |
x > –2,5 |
x ≤ –0,4 |
II |
–3, 0 |
x > 7 |
x > 8 |
x > 10 |
x ≤ 7 |
VI. Подведение итогов.
Домашнее задание: решить задачи № 33.27 (б, г); 33.30 (в, г); 33.35.