Поурочные разработки по Алгебре 8 класс
Урок 1 - ИССЛЕДОВАНИЕ ФУНКЦИЙ НА МОНОТОННОСТЬ
Цели: повторить изученные функции; ввести понятие убывающей и возрастающей функций; формировать умение определять какой (убывающей или возрастающей) является функция.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Для учащихся, не справившихся с самостоятельной работой, предлагается домой аналогичная работа.
1) Решить неравенства:
а) 9 < 6x – x2; б) 40x – 16x2 – 25 > 0; в) 2x2 + 6 > 0;
г) 9x2 + 3x ≥ 0; д) 17 + x2 ≤ 8x; е) 0,81 – x2 > 0.
2) При каких параметрах b уравнение x2 – bx – b + 3 = 0
а) не имеет корней;
б) имеет один корень.
Р е ш е н и е:
x2 – bx – b + 3 = 0;
a = 1, b = –b, c = 3 – b;
D = b2 – 4ac = b2 – 4(3 – b) = b2 + 4b – 12;
а) чтобы данное уравнение не имело корней необходимо выполнение условия D < 0.
Решим неравенство: b2 + 4b – 12 < 0;
B1 = –6, b2 = 2;
b ![]() (–6; 2).
(–6; 2).
б) чтобы данное уравнение имело один корень, необходимо выполнение условия D = 0.
В данном случае надо решить уравнение: b2 + 4b – 12 = 0;
B1 = –6, b2 = 2.
III. Актуализация знаний.
Вспомнить функции
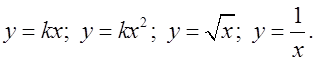
Построить на доске их графики (k > 0).
IV. Объяснение нового материала.
Учитель вводит понятие возрастающей и убывающей функций.
Далее каждая из построенных на доске функций рассматриваются на промежутке [1; 3].
V. Закрепление нового материала.
Устно разобрать задания № 32.1; 32.2; 32.3.
Письменно выполняются задания № 32.5; 32.6.
Если времени на уроке достаточно, можно предложить самостоятельно построить на координатной плоскости:
а) убывающую на интервале (–2; 4) функцию;
б) функцию, возрастающую на отрезке [–3; –1] и убывающую на интервале (–1; 2];
в) функцию, убывающую на интервале [–1; 1), возрастающую на отрезке [1; 3] и убывающую на интервале (3; 5).
VI. Подведение итогов.
Домашнее задание: изучить материал параграфа 32. Решить задание № 32.6; 32.7.