Поурочные разработки по Алгебре 8 класс
Урок 4 - ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ
Цели: закрепить умение решать квадратные уравнения; рассмотреть различные задания, решающиеся с помощью квадратного уравнения; проверить умение учащихся решать полные и неполные квадратные уравнения.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Для выполнения заданий к доске вызываются по два ученика. На местах учащиеся выполняют одно (на выбор).
1) Решить уравнения:
а) x2 – 13x + 22 = 0; б) (3x + 4)2 + (5x – 1)2 = 38 + x.
2) При каком значении a уравнение имеет один корень:
а) x2 + ax + 9 = 0; б) x2 + 3ax + a = 0.
3) Решить задачу:
а) Произведение двух натуральных чисел равно 273. Найдите эти числа, если одно из них на 8 больше другого.
б) Площадь прямоугольника равна 480 дм2. Найдите величины сторон данного прямоугольника, если его периметр равен 94 дм.
III. Решение задач.
1) Рассмотреть решение заданий № 25.37; 25.45; 25.44. Сильным учащимся предлагаются следующие задания:
2) При каком значении a данное уравнение
а) 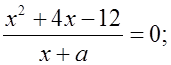 б)
б) 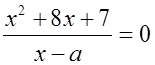 имеет только один корень?
имеет только один корень?
3) Решить уравнение:
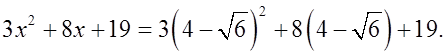
Р е ш е н и е:
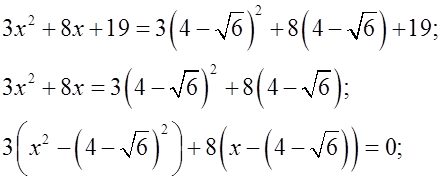
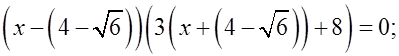
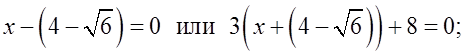
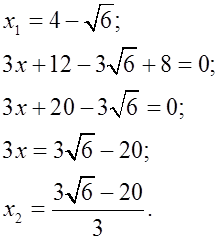
О т в е т: 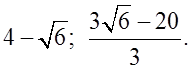
IV. Самостоятельная работа.
Вариант 1 1) 9x + 8x2 = –1 2) 3 + 3x2 = 4x 3) 25 – 10x + x2 = 0 4) 4x – 4x2 = 1 5) 3x2 – 4 = 0 6) 9x2 + 8 = 18x 7) 2x = –x2 – 1 8) 20x + 25x2 = –4 9) –1 – 4x2 = 0 10) 0,3x – x2 = 0 11) 12 – 17x – 5x2 = 0 |
Вариант 2 1) 2 – 9x2 = 0 2) –15 – 2x2 = –11x 3) –0,36 – x2 = 0 4) 16x + 64 = –x2 5) 13x + 3x2 = –14 6) 7x2 – 3x = 0 7) 5 = 2x – x2 8) 16 + x2 = 8x 9) 1 – 4x2 + 3x = 0 10) –12x + 4 = –9x2 11) 10x2 – 2 = x |
Вариант 3 1) 6 + 3x2 = 8x 2) 25 + 4х2 – 20х = 0 3) –2х2 + 3x = 0 4) 8x + 1 = –7х2 5) 1 + х2 = –2x 6) –х2 = 9 – 6x 7) 7 = 6х2 – 5 8) 13х – 14 + 3х2 = 0 9) – 8x – 16х2 = 1 10) –х2 = 0,4 11) 2х2 – 1 = 0 |
О т в е т ы:
Задание |
Вариант 1 |
Вариант 2 |
Вариант 3 |
1 |
–1 и |
|
нет корней |
2 |
нет корней |
3 и 2,5 |
нет корней |
3 |
5 |
нет корней |
0 и – 1,5 |
4 |
0,5 |
–8 |
–1 и |
5 |
|
–2 и |
–1 |
6 |
|
0 и |
3 |
7 |
–1 |
нет корней |
–0,5 и |
8 |
–0,4 |
4 |
2 и |
9 |
±0,5 |
1 и |
–0,25 |
10 |
0 и 0,3 |
|
0 и 2,5 |
11 |
0,6 и –4 |
0,5 и –0,4 |
|
V. Подведение итогов.
Домашнее задание: решить задания № 25.7; 25.43.