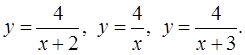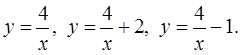Поурочные разработки по Алгебре 8 класс
Урок 1 - КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = f(x + l) + m, ЕСЛИ ИЗВЕСТЕН ГРАФИК ФУНКЦИИ y = f(x)
Цели: повторить правила построения графиков функций y = f(x + l) и f(x) + m, если известен график функции y = f(x); объяснить правило построения графика функции y = f(x + l) + m, если известен график функции y = f(x); развивать умение строить графики различных функций.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
К доске вызываются два ученика. Первый из них вместе с классом выполняет задание с карточки № 1, а второй (самостоятельно) – с карточки № 2. После того, как решена первая задача, разбирается решение второй. Затем, таким же образом, проводится работа по карточкам 3 и 4.
Карточка 1 Построить графики функций: y = 4x2, y = 4(x – 1) 2, y = 4(x + 2) 2. |
Карточка 2 Построить графики функций:
|
Карточка 3 Построить графики данных функций: y = 4x2, y = 4x2 – 5, y = 4x2 + 1 |
Карточка 4 Построить графики заданных функций:
|
III. Актуализация знаний.
Для самостоятельного решения предлагаются № 20.11; 20.12.
Учащиеся формулируют правило построения графиков функций y = f(x + l) и y = f(x) + m, если известен график функции y = f(x).
IV. Объяснение нового материала.
Учащимся предлагается построить график функции y = 4(x – 1)2 + 2. Проходит обсуждение построения данного графика. Формулируется правило построения графика функции y = f(x + l) + m, если известен график функции y = f(x).
Чтобы построить график функции y = f(x + l) + m, если известен график функции y = f(x), надо график функции f(x) сдвинуть по оси Ox на |l| единиц вправо, если l < 0 или влево, если l > 0, а затем сдвинуть получивший график по оси Oy на |m| единиц вверх, если m > 0, вниз, если m < 0.
Используя полученное правило, учитель показывает на доске построение график функции 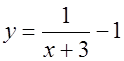 (в тетрадях данный график строится с помощью шаблонов).
(в тетрадях данный график строится с помощью шаблонов).
Затем учитель предлагает учащимся более рациональный способ решения подобных задач, т. е. использование вспомогательной системы координат.
Для функции y = 4(x – 1) 2 + 2:
1) выбираем вспомогательную систему координат с началом в точке (1; 2) (пунктирные прямые х = 1; у = 2).
2) Привяжем функцию y = 4x2, к новой системе координат таким образом: выбираем контрольные точки для функции y = 4x2, например, (0; 0); (1; 4); (–1; 4). Строим их в новой системе координат. Затем через полученные точки проведем параболу.
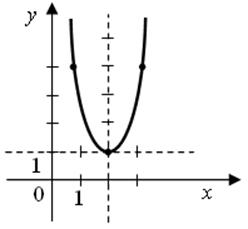
Получили второе правило построения графика функции y = f(x + l) + m.
Чтобы построить график функции y = f(x + l) + m, нужно перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые x = –l, y = m. Затем к новой системе привязать график функции y = f(x).
V. Закрепление нового материала.
1) Для закрепления материала учащимся предлагается построить с помощью шаблонов графики следующих функций:
а) y = x2, y = (x – 3) 2, y = (x – 3) 2 – 4;
б) y = –2x2, y = –2x2 + 5, y = –2(x – 1) 2 + 5;
в) 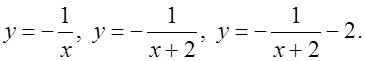
Для выполнения данного задания к доске вызываются трое учащихся, каждый из них выполняет построение на отдельной координатной плоскости. Учащиеся класса выполняют данное построение в тетрадях. При выполнении задания можно использовать любое правило.
2) Разобрать задания № 21.6; 21.7 (с помощью шаблонов), 21.16.
VI. Подведение итогов.
Домашнее задание: прочитать материал параграфа 21, выучить правило. Решить задачи № 21.5; 21.9; 21.8.