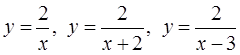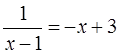КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = f(x + l), ЕСЛИ ИЗВЕСТЕН ГРАФИК ФУНКЦИИ y = f(x)

Цели: повторить правило построения графика функции y = f(x + l), если известен график функции y = f(x); объяснить правило построения графика функции y = f(x) + m, если известен график функции f(x); формировать умение строить графики различных функций.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

Четырем учащимся даются индивидуальные задания на карточках.

Карточка 1 Построить графики заданных функций: y = –3x2, y = –3(x – 1) 2, y = –3(x + 2) 2.	Карточка 2 Построить графики заданных функций:
Карточка 3 Решить уравнение графическим способом: 2(x + 2) 2 = 2x + 4	Карточка 4 Решить уравнение графическим способом:

III. Актуализация знаний.

Пока учащиеся у доски выполняют свои задания, остальные проверяют домашнюю работу.

При проверке каждого задания повторяется правило построения функции y = f(x + l), если известен график функции f(x).

После этого выполняются № 19.11; 19.12; 19.33.

Учащиеся, выполнившие индивидуальные задания, сдают свои работы.

IV. Объяснение нового материала.

На доске на одной координатной плоскости пунктирной линией построить график функции y = –x2, сплошной линей построить графики функций y = –x2 + 1 и y = –x2 – 3. На другой координатной плоскости пунктирной линией строится график функции 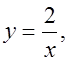а сплошной линией график функции 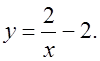Построения (поточечное) выполняются учениками. После всех построений ученики самостоятельно делают выводы, и стараются сформулировать правило построения графика функции y = f(x) + m, если извете график функции f(x). Помогает им правило прошлого урока.

Чтобы построить график функции y = f(x) + m, если известен график функции y = f(x), надо график функции f(x) сдвинуть по оси Oy на |m| единиц вверх, если m > 0 или вниз, если m > 0.

V. Закрепление нового материала.

1) Для закрепления материала учитель на доске работает с помощью шаблона функции y = x2. На координатной плоскости данный шаблон переносится в разные позиции относительно оси Ox и относительно оси Оу, а ученики должны назвать функцию, определяющую данный график.

2) Разобрать задания № 20.2; 20.5; 20.7 (г); 20.8 (г); 20.17; 20.20; 20.25. При наличии времени решить задачи № 20.26; 20.39.

VI. Подведение итогов.

Домашнее задание: прочитать материал параграфа 20, выучить правило. Решить задачи № 20.1; 20.6; 20.16; 20.19.