Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Итоги контрольной работы - Урок 2 - Системы уравнений
Цели: сообщить результаты работы; рассмотреть типичные ошибки; разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
III. Ответы и решения
Вариант 1
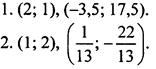
3. 4 см и 10 см.
4. а, б - построено.
5. Построено.
Вариант 2
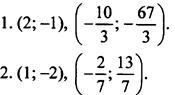
3. 6 см и 7 см.
4. а, б - построено.
5. Построено.
Вариант 3
![]()
2. 14 и 11.
3. а, б - построено.
4. Построено.
Вариант 4
![]()
2. 17 и 11.
3. а, б - построено.
4. Построено.
Вариант 5
1а. Для решения системы уравнений  запишем ее в виде
запишем ее в виде ![]() В первом уравнении произведение двух множителей равно нулю. Поэтому один из этих множителей равен нулю. Получаем две системы линейных уравнений:
В первом уравнении произведение двух множителей равно нулю. Поэтому один из этих множителей равен нулю. Получаем две системы линейных уравнений:
а) ![]() ее решение x = 1, y = -1;
ее решение x = 1, y = -1;
б) ![]() ее решение х = -2, y = -5.
ее решение х = -2, y = -5.
Ответ: (1; -1); (-2; -5).
1б. Для решения системы уравнений 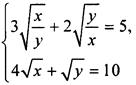 в первом уравнении введем новую переменную:
в первом уравнении введем новую переменную: ![]() Получаем уравнение:
Получаем уравнение: ![]() или 3t2 - 5t + 2 = 0, корни которого t = 1 и t = 2/3. Вернемся к старым неизвестным. Получаем две системы уравнений:
или 3t2 - 5t + 2 = 0, корни которого t = 1 и t = 2/3. Вернемся к старым неизвестным. Получаем две системы уравнений:
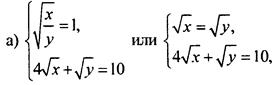 откуда √x = √y = 2 и х = у = 4;
откуда √x = √y = 2 и х = у = 4;
 откуда
откуда ![]()
![]()
Ответ: ![]()
2. В первом уравнении системы 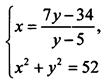 выделим целую часть и запишем его в виде
выделим целую часть и запишем его в виде ![]() Так как х и y - целые числа, то у - 5 = 1 (тогда у = 6 и х = 8) или у - 5 = -1 (тогда у = 4 и х = 6). Легко проверить, что второму уравнению системы удовлетворяет только решение (6; 4).
Так как х и y - целые числа, то у - 5 = 1 (тогда у = 6 и х = 8) или у - 5 = -1 (тогда у = 4 и х = 6). Легко проверить, что второму уравнению системы удовлетворяет только решение (6; 4).
Ответ: (6; 4).
3. Пусть скорость велосипедиста х км/ч и длина пути у км. Запишем условия задачи: 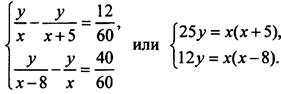 Разделим уравнения друг на друга:
Разделим уравнения друг на друга: ![]() - и найдем х = 20. Например, из первого уравнения определим
- и найдем х = 20. Например, из первого уравнения определим ![]()
Ответ: 20 км/ч и 20 км.
4а. В уравнении |у2 – х2| = у + х учтем, что у + х ≥ 0, т. е. у ≥ -х. Запишем уравнение в виде (у + х)|у - х| = у + х или (у + х)(|у - х| - 1) = 0, откуда y + х = 0 (т. е. y = -х) и |у - х| - 1 =0, или |у - х| = 1, или y - x = ±1 (т. e. y = х ± 1).
Построим прямую у = -х и две параллельные прямые у = х ± 1 для у > -х. Получаем график данного уравнения:
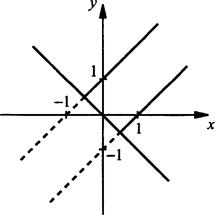
Ответ: построено.
4б. Неравенство |3х - у + 1| ≤ 2 запишем в виде -2 ≤ 3х - у + 1 ≤ 2, или -3 ≤ 3х - у ≤ 1, или 3 ≥ у - 3х ≥ -1, или 3х - 1 ≤ у ≤ 3х + 3. Построим две параллельные прямые у = 3х - 1 и у = 3х + 3. Легко проверить, что данному неравенству удовлетворяет множество точек, расположенных между этими прямыми. Получаем график данного неравенства:
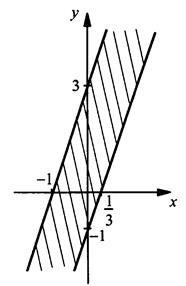
Ответ: построено.
Вариант 6
1а. Для решения системы уравнений 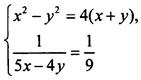 запишем ее в виде
запишем ее в виде ![]() В первом уравнении произведение двух множителей равно нулю. Поэтому один из этих множителей равен нулю. Получаем две системы линейных уравнений:
В первом уравнении произведение двух множителей равно нулю. Поэтому один из этих множителей равен нулю. Получаем две системы линейных уравнений:
![]() ее решение х = 1, у = -1;
ее решение х = 1, у = -1;
![]() ее решение х = -7, у = -11.
ее решение х = -7, у = -11.
Ответ: (1; -1); (-7; -11).
16. Для решения системы уравнений 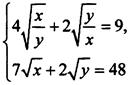 в первом уравнении введем новую переменную
в первом уравнении введем новую переменную ![]() Получаем уравнение:
Получаем уравнение: ![]() или 4t2 – 9t + 2 = 0, корни которого t = 2 и t = 1/4. Вернемся к старым неизвестным. Получаем две системы уравнений:
или 4t2 – 9t + 2 = 0, корни которого t = 2 и t = 1/4. Вернемся к старым неизвестным. Получаем две системы уравнений: 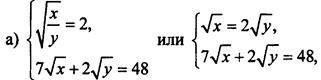 откуда √x = 6, √у = 3 и х = 36, у = 9;
откуда √x = 6, √у = 3 и х = 36, у = 9;
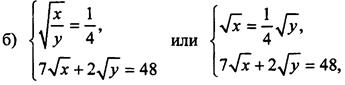 откуда
откуда ![]()
![]()
Ответ: ![]()
2. В первом уравнении системы 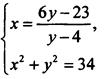 выделим целую часть и запишем его в виде
выделим целую часть и запишем его в виде ![]() Так как х и у - целые числа, то у - 4 = 1 (тогда у = 5 и х = 7) или у - 4 = -1 (тогда у = 3 и х = 5). Легко проверить, что второму уравнению системы удовлетворяет только решение (5; 3).
Так как х и у - целые числа, то у - 4 = 1 (тогда у = 5 и х = 7) или у - 4 = -1 (тогда у = 3 и х = 5). Легко проверить, что второму уравнению системы удовлетворяет только решение (5; 3).
Ответ: (5; 3).
3. Пусть скорость велосипедиста х км/ч и длина пути у км. Запишем условия задачи: 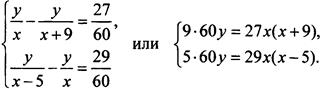 Разделим уравнения друг на друга:
Разделим уравнения друг на друга: ![]() - и найдем х = 20. Например, из первого уравнения определим
- и найдем х = 20. Например, из первого уравнения определим ![]()
Ответ: 20 км/ч и 29 км.
4а. В уравнении |у2 - х2| = у - х учтем, что у - х ≥ 0, т. е. у ≥ х. Запишем уравнение в виде (у - х)|у + х| = у - х или (у - х)(|у + х| - 1) = 0, откуда у - х = 0 (т. е. у = х) и |у - х| - 1 = 0, или |у + x| = 1, или у + х = ±1 (т. е. у = -х ± 1). Построим прямую у = х и две параллельные прямые у = -х ± 1 для у > х. Получаем график данного уравнения:
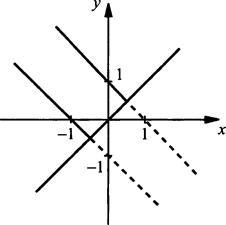
Ответ: построено.
4б. Неравенство |2х + у - 2| ≤ 1 запишем в виде -1 ≤ 2х + у - 2 ≤ 1 или -2х + 1 ≤ у ≤ -2х + 3. Построим две параллельные прямые у = -2х + 1 и у = -2х + 3. Легко проверить, что данному неравенству удовлетворяет множество точек, расположенных между этими прямыми. Получаем график данного неравенства:
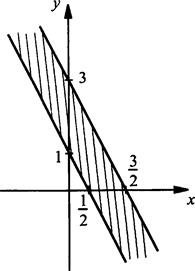
Ответ: построено.