Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМЕ ТРЕУГОЛЬНИК - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цель деятельности учителя |
Создать условия для систематизации знаний по теме “Треугольник”, повторения основных свойств, признаков треугольника, для подготовки к сдаче ГИА |
|
|
Термины и понятия |
Равенство и подобие треугольников, сумма углов треугольника, равнобедренный треугольник, прямоугольный треугольник, площадь треугольника |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в паре. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Задания для самостоятельной работы, групповой работы, домашней работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Систематизировать теоретический материал |
(И) - Укажите номера верных утверждений. 1) Диагонали трапеции точкой пересечения делятся пополам. 2) Вписанный угол измеряется половиной дуги, на которую он опирается. 3) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - прямоугольник. 4) Сумма внутренних углов треугольника равна 180°. 5) В равнобедренной трапеции диагонали равны. 6) Если две параллельные прямые пересечены секущей, то биссектрисы накрест лежащих углов параллельны. 7) Около любого четырёхугольника можно описать окружность. 8) Окружность нельзя вписать в любой треугольник. 9) В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°. 10) Любая хорда, проходящая через центр окружности, является ее диаметром. 11) Диагонали ромба равны. 12) Перпендикулярные прямые пересекаются под прямым углом. 13) В прямоугольном треугольнике любой катет меньше гипотенузы. 14) Треугольник со сторонами 3, 5, 6 существует. 15) Диагонали прямоугольника равны. 16) Сумма углов выпуклого четырехугольника равна 300°. Ответы: 2, 4, 5,6, 9, 10, 12, 13, 14, 15 |
|
|
II этап. Решение задач |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Совершенствовать навыки решения задач |
(Г) Каждой группе предлагается решить три задачи. Далее группы представляют решения, обсуждают, записывают лучшее. 1. В треугольниках АВС и DEK АВ = DE, АС = DK, BP = ЕМ; Р и М - середины сторон АС и DK. 1) Докажите, что треугольник АВС равен треугольнику DEK. 2) Найдите SABC, если ЕМ = 3 см, DK = 4√2 см, ∠EMK = 135°. 2. В треугольниках АВС и А1В1С1 АС = А1С1, ВС = В1С1, BD = B1D1; BD и B1D1 - высоты треугольников, причем точки D и D1 лежат на отрезках АС и А1С1. 1) Докажите, что треугольник АВС равен треугольнику А1B1C1. 2) Найдите радиус окружности, описанной около треугольника B1D1C1 если известно, что BD = 6 см, DC = 8 см. 3) Найдите угол А1C1B1, если BD = 6 см, DC = 8 см. 3. В треугольнике АВС АВ = 14 см, АС = 15 см, ВС = 13 см. Найдите: 1) длину меньшей высоты треугольника; 2) площадь треугольника ADC, если AD - биссектриса треугольника АВС; 3) медиану АЕ треугольника АВС. |
|
|
III этап. Самостоятельная работа с самопроверкой |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Проверить готовность учащихся к сдаче ГИА (модуля геометрии) |
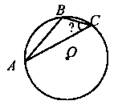
(И) Вариант I 1. Один из внешних углов треугольника равен 120°. Найдите сумму углов треугольника, не смежных с ним. 2. Дан треугольник АВС. Найдите его периметр, если длины его средних линий равны 5, 7 и 9. 3. Используя рисунок, найдите градусную меру угла С, если угол А = 14°, а градусная мера большей из дуг АС = 236°
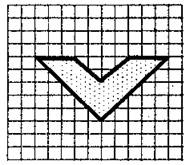
4. Найдите площадь фигуры, изображенной на рисунке. (1 клеточка = 1 см2.)
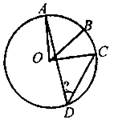
Вариант II 1. Дан прямоугольный треугольник АВС, угол С - прямой, угол В = 26°. Найдите величину внешнего угла при вершине А. 2. Найдите большее основание трапеции, если длина ее средней линии равна 11, а длина меньшего основания равна 7. 3. Используя рисунок, найдите градусную меру угла D, если угол ВОС = 40°, а градусная мера меньшей из дуг АВ = 58°.
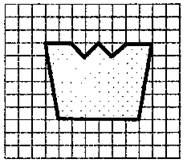
4. Найдите площадь фигуры, изображенной на рисунке. (1 клеточка = 1 см2.)
Ответы: Вариант I: 1. 120°; 2. 42; 3. 48°; 4. 21. Вариант II: 1. 116°; 2. 15; 3.49°; 4. 40 |
|
|
IV этап. Итоги урока. Рефлексия |
|||||||||
|
Деятельность учителя |
Деятельность учащихся |
||||||||
|
(Ф/И) - Какие свойства треугольников повторили на уроке? - Что оказалось для вас наиболее сложным? - Оцените свою работу и работу в группе |
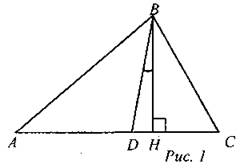
(И) Домашнее задание: решить задачи. 1. В треугольнике АВС АС = ВС. Внешний угол при вершине В равен 146. Найдите угол С. Ответ дайте в градусах. 2. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6. 3. Сторона ромба равна 8, а расстояние от центра ромба до нее равно 2. Найдите площадь ромба. 4. В треугольнике АВС угол С равен 90°, АС = 12, 5. Укажите номера верных утверждений. 1) В тупоугольном треугольнике все углы тупые. 2) В любом параллелограмме диагонали точкой пересечения делятся пополам. 3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. 6. В треугольнике АВС углы А и С равны 40° и 60° соответственно (рис. 1). Найдите угол между высотой ВН и биссектрисой BD.
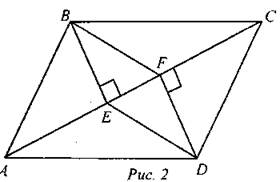
7. В параллелограмме ABCD проведены перпендикуляры BE и DF к диагонали АС (рис. 2). Докажите, что BFDE - параллелограмм.
|
||||||||
|
Задание |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
Ответ: |
112 |
2√3 |
32 |
28 |
33 |
10 |
- |
||