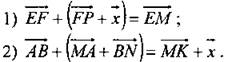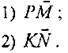СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ - ВЕКТОРЫ

Цель деятельности учителя

Создать условия для введения понятия суммы двух векторов, рассмотрения законов сложения векторов, обучения построению суммы двух данных векторов с использованием правила треугольника и параллелограмма

Термины и понятия

Вектор, сумма векторов, разность векторов, правило треугольника, правило параллелограмма

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять векторы, находить сумму и разность векторов, строить сумму и разность векторов

Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: выстраивают аргументацию, участвуют в диалоге.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы_______

• Задания для парной и фронтальной работы

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Проверить правильность выполнения домашнего задания

(Ф/И)

Проверить решение задачи № 752.

а) Если то и .

Ответ: верно.

б) Если то то есть коллинеарные.

Ответ: верно.

в) Если то , значит - не может быть.

Ответ: неверно.

г) Если , то не обязательно , так как может быть, что .

Ответ: неверно.

д) Если , то , так как сонаправлен с любым вектором.

Ответ: верно

II этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Научить строить сумму векторов, используя правило треугольника и правило параллелограмма

(Ф)

1. Рассмотреть пример п. 82 о перемещении материальной точки из точки А в точку В, а затем из точки В в точку С (рис. 249). Записать:

2. Ввести понятие суммы двух векторов (рис. 250); правило треугольника

3. Устно провести доказательство по рис. 251.

4. Записать в тетрадях:

1) для любого вектора справедливо равенство

2) если А, В и С - произвольные точки, то (правило треугольника).

5. Выполнить практическое задание № 753.

6. Рассмотреть законы сложения векторов.

7. Рассмотреть правило параллелограмма (рис. 252) и частное использование этого правила в физике, например при сложении двух сил

III этап. Практическая работа. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф/И)

1. Начертите попарно неколлинеарные векторы Постройте векторы.

2. Решите № 759 (а) без помощи чертежа.

3. Упростите выражения:

(П)

4. Найдите вектор из условий:

5. Докажите, что четырехугольник ABCD - параллелограмм, если где Р и x - произвольные точки плоскости

№ 759 (а).

Докажите, что

Доказательство:

- равенство верно.

Доказательство:

получим, что векторы равны, а это значит, что тогда по признаку параллелограмма ABCD - параллелограмм

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

-Какие правила для построения суммы векторов изучили на уроке? В чем их отличие?

- Составьте синквейн к уроку

(И) Домашнее задание: № 754, 759 (б) (без чертежа), 763 (б, в)